Torneo de las ciudades, 2016 (Primavera, nivel A junior) Se dirige a una edad de: 12/15
a) ¿Existen enteros a y b de forma que la ecuación x2 + ax + b = 0 no tiene soluciones reales y la ecuación [x2] + ax + b = 0 sí que tiene al menos una solución real?
b) ¿Existen enteros a y b de forma que la ecuación x2 + 2ax + b = 0 no tiene soluciones reales y la ecuación [x2] + 2ax + b = 0 sí que tiene al menos una solución real?
(La función [k] denota la parte entera de k, es decir, el entero más grande que está por debajo de k.)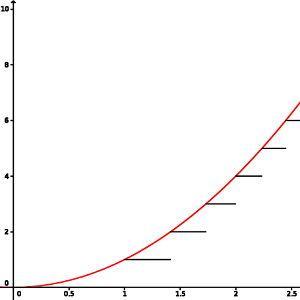
Solución:
Para resolver bien este problema, conviene saber resolver con soltura las ecuaciones de segundo grado, y conocer la fórmula de las soluciones, en especial aplicadas a las expresiones del problema.
También conviene saber que la forma de representar las fórmulas de segundo grado es una parábola, cuyo punto más bajo (o más alto, en otros casos) es el vértice, que se calcula dividiendo el opuesto del coeficiente de la x entre el doble del coeficiente de la x2.
Apartado a
Para que una ecuación de segundo grado no tenga solución, debe suceder que la expresión a2 – 4b sea negativa, porque en este caso sería lo que aparecería dentro de la raíz con la que calculamos la solución, y eso significa que no habría ningún número real que lo cumpliese.
En ese caso, 4b sería mayor que a2. Pero, al tomar parte entera, es como quitar un valor decimal a x2, de forma que es como si tomamos un valor de b algo menor, y para ese valor, puede que a2 sea algo mayor que 4b. Al mismo tiempo, x2 debe ser un número decimal con una parte decimal algo grande, para que podamos quitar una cantidad relativamente grande a b.
Podemos ajustar la ecuación a varios valores, de forma que b sea mayor que un cuarto de a2, pero al quitarle un poco ya no. Por ejemplo, si a = 3 y b =3 , está claro que a2 – 4b = -3, negativo, pero si a b le quitamos un número algo mayor de 3/4 = 0.75, tendríamos posibilidades de tener raíces. En este caso, casualmente, el valor x = -4/3 es solución de la ecuación, ya que [x²] + ax + b = [16/9] + 3*(-4/3) + 3 = 1 + -4 + 3 = 0. Encontrar este tipo de valores puede requerir probar varias posibilidades, pero hay muchos disponibles. Observa que la parte decimal de x2 en ese caso es 7/9, aproximadamente 0.778, algo mayor que 0,75.
Lo que parece claro es que para que a2 y 4b estén lo más cerca posible, a debe ser impar, como veremos, con los pares no funciona (apartado b).
Pero algunos valores no dan resultado. Por ejemplo, si a = 1, entonces b = 1 (lo más cerca posible de la cuarta parte de a²), pero en ese caso, el vértice de la parábola (el punto más bajo) está en x = -1/2, es decir, que x2 = 1/4, y su parte entera es cero. Si buscamos soluciones, entonces 0 + x + 1 debe ser cero, y en ese caso, x = -1 y la ecuación no funciona.
Usemos otro valor, si a = 5, entonces b = 7, y el vértice está en x = -5/2, y eso significa que la parte entera de x2 es 6, tanto en el vértice como cerca de él. Por tanto, la ecuación cerca del vértice será 6 + 5x + 7 = 0, por lo que x = -13/5 es una solución. En efecto, para ese valor podemos comprobar que la ecuación da cero. Es decir, que otra solución sería que a = 5, b = 7 y x = -13/5.
Si queremos que la x sea positiva, debemos usar valores negativos de a, ya que es imposible que sea cero ninguna de las igualdades si todos los números implicados son positivos.
Otra posibilidad es dibujar la gráfica de la parábola, de forma que el vértice esté cerca de la x (el vértice de la parábola x2 + 3x + 3 está en el punto ( – 1.5, 0,75)) y trabajar sólo con la parte N + ax + b en los intervalos adecuados (procurando que estemos cerca del vértice, y N es la parte entera de la x del vértice al cuadrado).
Apartado b
En este apartado, la respuesta es que no, aunque sea muy similar al anterior. Ahora el coeficiente de la x debe ser par y eso lo cambia todo, ya que ahora la expresión que debe ser negativa es (2a)2 – 4b = 4a2 – 4b, es decir, que b debe ser mayor que a2, y como es un número entero, resulta que debe ser como mínimo una unidad mayor, por lo que aunque le quitemos un número decimal, que siempre es menor que uno, no llegará a ser menor.
Otra forma de razonarlo es que, puesto que b > a2, b es mayor o igual que a2 + 1, y por tanto, [x2] + 2ax + b es mayor que x2 + 2ax + b – 1, que es mayor o igual que x2 + 2ax + a2 + 1 – 1 = (x + a)2 (observa que la expresión es exactamente igual que el cuadrado de la suma), que sabemos que siempre es mayor o igual que cero, por lo que [x2] + 2ax + b es mayor que cero para todo valor de x.