Olimpiada Junior de los Balcanes, 2017. Se dirige a una edad de: 16 años
Encuentra todos los conjuntos de seis números enteros positivos consecutivos que cumplen que si multiplicamos dos de ellos y le sumamos el producto de otros dos, obtenemos lo mismo que si multiplicamos los otros dos restantes.
Hay que encontrar todos los conjuntos y demostrar que no existen más.
Soilución: Aquí
Olimpiada del Cono Sur, primer problema del año 2017
Diremos que un número es guayaquileano si la suma de los dígitos de n es igual que la suma de los dígitos de n².
Encuentra todos los posibles valores que puede dar la suma de las cifras de un número guayaquileano.
Solución:
Continue reading Solución a números guayaquileanos
¿Cuándo descubriste que te gustaban las Matemáticas?
Me han gustado desde pequeño. Mi madre, al ver que me gustaban, me enseñaba matemáticas un poco adelantadas al curso en el que estaba. Mientras pudo adelantarme lo hizo, y yo lo recibía muy bien. Cuando ella llegó a su límite ya había aportado lo suficiente como para que yo continuara el camino.
¿Cómo recuerdas tu paso por la licenciatura o el grado en Matemáticas?
En general muy bueno. Yo hice la licenciatura, en Granada, y sin duda repetiría. Es cierto que los comienzos fueron malos, pero por mi culpa (me confié). Cuando conseguí recuperarme de ese primer año malo disfruté muchísimo en mis estudios. Hay que estudiar y trabajar mucho, pero si te gustan las matemáticas merece mucho la pena tanto esfuerzo.
¿Quién es tu matemático/matemática preferido/preferida?
Teniendo en cuenta que soy el autor de https://gaussianos.com, está claro que Gauss es uno de mis matemáticos preferidos. También Pierre de Fermat, siempre tuve debilidad por él y por la rama de las matemáticas en la que más destacó: la teoría de números.
¿Qué te gusta más de las Matemáticas?
Su capacidad para sorprenderme. Llevo años dedicado a ellas (estudiándolas, dando clases a todos los niveles, 11 años divulgando a través de internet…) y todavía hoy sigo encontrando problemas interesantes, descubriendo teoremas curiosos y conociendo historias de matemáticas y matemáticos dignas de ser contadas. Las matemáticas son un mundo maravilloso.
¿Dónde hablaste por primera vez en público sobre Matemáticas?
En enero de 2011. Me invitaron a dar un taller en la universidad en Santander dentro de un programa que tienen dedicado a la divulgación de las matemáticas. El taller trataba sobre blogs y matemáticas, y la verdad es que salió todo muy bien. Estoy muy agradecido, ya que a partir de ahí tuve la oportunidad de dar una buena cantidad de charlas de divulgación de matemáticas que han complementado el trabajo que realizo en este sentido en internet desde hace años.
Olimpiada del Cono Sur, primer problema del año 2017
Diremos que un número es guayaquileano si la suma de los dígitos de n es igual que la suma de los dígitos de n².
Encuentra todos los posibles valores que puede dar la suma de las cifras de un número guayaquileano.
Solución: Aquí
Mathcounts, ronda final, séptimo problema de 2017 Se dirige a una edad de: 13
En una granja, cien pollitos se distribuyen pacíficamente en una circunferencia. En un momento determinado, simultaneamente, cada pollito picotea al pollito de la izquierda o de la derecha, (a uno de los dos aleatoriamente).
¿Qué número de pollitos se estima que no hayan recibido ningún picotazo?
¿Cuándo descubriste que te gustaban las Matemáticas?
Desde siempre, creo que fue un flechazo, desde pequeña… se me daban bien, me divertía… un amor a primera vista.
¿Cómo recuerdas tu paso por la licenciatura o el grado en Matemáticas?
Fue una época feliz, tranquila, esforzada, de estudio intenso, de trabajo en equipo… de hacer a amigas y amigos que siguen estando presentes en mi día a día.
¿Quién es tu matemático/matemática preferido/preferida?
Porque soy topóloga y porque el conjunto de Cantor ha estado muy presente en mi tema de investigación, Georg Cantor siempre ha sido una especie de ídolo para mí. Su vida, sus matemáticas, su lucha, su ¿locura? (o su genialidad) me han fascinado desde siempre. Ya sé que la pregunta era en singular, pero necesito hablar de Sofia Kovalevskaya. La he ido conociendo gracias a otra matemática (Michèle Audin) que le ha dedicado un magnífico libro. Sofia fue una matemática extraordinaria y una mujer extraordinaria: con una capacidad intelectual fuera de lo común, nihilista, feminista, luchadora… genial.
¿Qué te gusta más de las Matemáticas?
Su belleza, la ‘seguridad’ que transmiten y al mismo tiempo las ‘sorpresas’ que encierran. Su capacidad de ‘engancharte’ y el placer que producen cuando consigues comprender algo realmente complejo…
¿Dónde hablaste por primera vez en público sobre Matemáticas?
En mi propia Facultad, en una serie de conferencias divulgativas que organizaba mi amigo y colega Raúl Ibáñez.
Mathcounts, ronda final, séptimo problema de 2017 Se dirige a una edad de: 13
En una granja, cien pollitos se distribuyen pacíficamente en una circunferencia. En un momento determinado, simultaneamente, cada pollito picotea al pollito de la izquierda o de la derecha, (a uno de los dos aleatoriamente).
¿Qué número de pollitos se estima que no hayan recibido ningún picotazo?
Solución: Aquí
Primer nivel de la Olimpiada de Mayo, 2016. Se dirige a una edad de: 12 años
A cada número de tres dígitos Matías le sumó el número que se obtiene invirtiendo sus dígitos.
Por ejemplo, al número 927 le sumó el 729.
Calcular en cuántos casos el resultado de la suma de Matías es un número con todos sus dígitos impares.
Solución:
Continue reading Solución a dígitos impares
¿Cuándo descubriste que te gustaban las Matemáticas?
Desde niño. Aprendí las operaciones elementales antes de ir a la escuela.
¿Cómo recuerdas tu paso por la licenciatura o el grado en Matemáticas?
Recuerdo que casi me quitan mi amor por las matemáticas. Empecé a disfrutar de ellas cuando dejé la facultad.
¿Quién es tu matemático/matemática preferido/preferida?
Sin duda Leonhard Euler, seguido de cerca por Gauss.
¿Qué te gusta más de las Matemáticas?
La elegancia y la belleza de los problemas históricos de la Teoría de Números. ¿Hay algo comparable a la magia de los números primos?
¿Dónde hablaste por primera vez en público sobre Matemáticas?
Fuera de las clases, en una conferencia preparatoria para los estudiantes de selectividad sobre los Fundamentos de la Matemática. En esa época, 1977, en la prueba de selectividad había una conferencia oral y y los alumnos tenían que resumir sus contenidos y responder preguntas sobre ellos. Yo acababa de terminar la licenciatura y tenía sólo 5 o 6 años más que los asistentes.
Primer nivel de la Olimpiada de Mayo, 2016. Se dirige a una edad de: 12 años
A cada número de tres dígitos Matías le sumó el número que se obtiene invirtiendo sus dígitos.
Por ejemplo, al número 927 le sumó el 729.
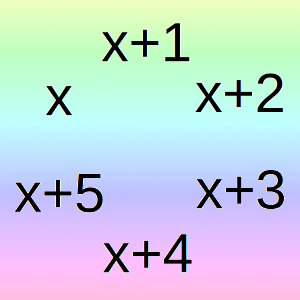
Calcular en cuántos casos el resultado de la suma de Matías es un número con todos sus dígitos impares.
Solución: Aquí