¿Realmente creías que te ibas a escapar? Pensabas que llegar a la Universidad te permitiría estudiar única y exclusivamente lo que te apasionaba, dejarte de asignaturas farragosas e incómodas y disfrutar de batallitas, ensuciarte las manos con rasquetas, pinceles y objetos arqueológicos fantásticos.
Pues no. Siento decepcionarte pero no vas a dejar atrás esas materias que te costaban más sacar adelante. El conocimiento de las llamadas “ciencias puras” son un recurso muy habitual enla arqueología de campo. La arqueología es una ciencia que se vale del conocimiento de otras muchas ciencias; y las matemáticas es una de ellas.
Las cosas son números
Una frase atribuída a Pitágoras, ése filósofo griego del que muchos habremos oído 
hablar en la secundaria (o el bachillerato) y que adquiere cierto protagonismo a la hora de representar una Unidad Estratigráfica del yacimiento sobre un plano. Por lo general, el yacimiento está bajo una gran cuadrícula formada por coordenadas recogidas con GPS o con una estación total.
La cuadrícula en arqueología de campo permite posteriormente representar los acontecimientos arqueológicos (tales como Unidedades estratigráficas, objetos encontrados, estructuras, etc.) sobre un plano. A partir de las coordenadas recogidas en la cuadrícula, establecemos la localización del acontecimiento que queremos representar y lo hacemos de manera proporcional tomando sus medidas.
Pero, ¿Qué pasa si me salgo de esta gigantesca cuadrícula?
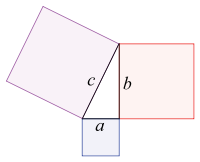
¿Y si tengo que dibujar una unidad estratigráfica fuera del área de excavación? Esto es algo bastante habitual. Cuando se elabora el área de excavación se realiza con el objetivo de abarcar toda la zona potencialmente excabable. Sin embargo, en ocasiones, las propias evidencias te llevan más allá de la red de coordenadas. ¿Entonces? Es cuando hacemos un llamamiento a Pitágoras. Por si no te acuerdas de nada salvo que era un griego de la antigüedad, ha pasado a la historia por darle el nombre a un teorema matemático que dice lo siguiente:
En un triángulo rectángulo, la suma de los cuadrados de los catetos (a y b) es igual al cudrado de la hipotenusa (c)
Con este teorema tenemos el probelma de la cuadrícula resuelto. Lo que tienes que hacer es lo siguiente:
1. Tomas la última piqueta de la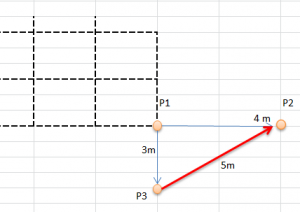 
cuadrícula y con una cuerda te alejas 4 metros justos de manera vertical y hacia la zona donde se encuentra el dibujo que quieres representar en planta y donde no hay cuadrícula.
2. Luego desde la misma piqueta de donde has empezado, te alejas 3 metros pero hacia el horizonte.
3. Ahora tienes una linea paralela de 4 metros y otra perpendicular de 3. Si Pitágoras estaba en lo cierto (que lo estaba) al juntar los dos puntos que quedan sueltos conseguirás una línea de 5 metros y, por ende, un triángulo rectángulo precioso. Es decir, media cuadrícula. ¡Bravo! Viva Pitágoras.
Para que veas que siempre encontrarás una utilidad a un conocimiento que pensabas que no te iba a servir de nada. ¡Las mates molan! 🙂