Solución a un punto en un cuadrado

Olimpiada Telemática Catalana (Olitele) 2016
Se dirige a una edad de: 16-17 años

Sea E un punto interior de un cuadrado ABCD que cumple que su distancia al vértice B es el doble que al vértice A, y la distancia al vértice C es triple que al vértice A.

Encuentra la medida en grados del ángulo AEB.

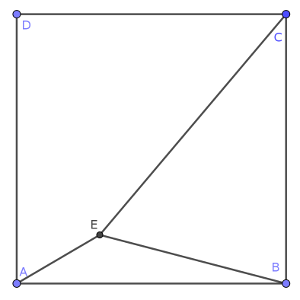
Solución:
Este problema es para hacer en casa, ya que el concurso Olitele es a través de Internet.

La medida del ángulo es independiente de la escala que se use para medir el cuadrado, así que podemos suponer que mide una unidad de lado (o cualquier otra cantidad), y la demostración no perderá generalidad.

Hemos estudiado varias vías de ataque, pero creemos que la más directa (aún así, es larga) consiste en estudiar el problema con vectores. Probablemente, vistas las soluciones, exista una forma de estudiar el problema con métodos puramente geométricos, pero no se nos ocurre ninguna evidente.

Así, si suponemos que el cuadrado mide la unidad, y las coordenadas de E son los valores (x, y), el punto A podríamos situarlo en el (0, 0) y el B en el (1, 0). Claramente, el C sería (1, 1).

La relación de distancias corresponde a las distancias de E con A, B y C, que corresponde a los tamaños de los vectores (x, y), (1 – x, y) y (1 – x, 1 – y). Puesto que es más cómodo plantearlo sin raíces, elevaremos al cuadrado, con lo que hay dos relaciones:

4x² + 4y² = (1 – x)² + y²

9x² + 9y² = (1 – x)² + (1 – y)²

Desarrollando los cuadrados y pasando todos los términos al primer término, las expresiones quedan como dos ecuaciones de segundo grado:

3x² + 3y² + 2x – 1 = 0

8x² + 8y² +2x +2y – 2 = 0

Se puede intuir que las dos ecuaciones corresponden a sendas circunferencias, por lo que es posible que haya dos puntos con esas características. Para resolverlas, conviene combinarlas para eliminar la parte de segundo grado de una de ellas, despejar y sustituir en la más sencilla.

De la primera, 24x² + 24y² + 16x – 8 = 0.

De la segunda, 24x² + 24y² +6x +6y – 6 = 0.

Restando la primera menos la segunda ordenadamente, tenemos 10x – 6y – 2 = 0. Es posible que os hayan contado que esta recta se llama la recta radical de dos circunferencias. Se simplifica a 5x – 3y = 1.

Ahora, en la recta, vamos a despejar la y y sustituir en la ecuación 3x² + 3y² + 2x – 1 = 0, la más sencilla de las dos obtenidas anteriormente. Claramente, y = (5/3)x – 1/3.

Para sustituir con comodidad, vamos a multiplicar la ecuación por 3, así el coeficiente de y² será 9 y no quedarán fracciones. La ecuación en la que voy a sustituir queda 9x² + 9y² + 6x – 3 = 0, y como 3y = 5x – 1, al elevar al cuadrado, tenemos que 9y² = 25x² – 10x + 1, por lo que la expresión al sustituir se transforma en :

9x² + 25x² – 10x + 1 + 6x – 3 = 0

Y esta expresión es una ecuación de segundo grado, 34x² – 4x – 2 = 0, que se puede simplificar dividiendo entre 2 a 17x² – 2x – 1 = 0. Lamentablemente, no tiene soluciones enteras, pero sí irracionales, serían x = (2 + raíz(72))/34 = (1 + 3raíz(2))/17 y la solución negativa (1 – raíz(2))/17, que no sería válida en este caso, porque caería fuera del cuadrado inicial.

Para obtener la y, trabajaríamos en la expresión 3y = 5x – 1, obteniendo que 3y = (5 + 15raíz(2))/17 – 1 = (15raíz(2) – 12)/17. Como es divisible entre 3, tenemos que y = (5raíz(2) – 4)/17, que también es positivo.

Ahora vemos que si hubiésemos tomado el cuadrado 17 unidades mayor, no tendríamos que trabajar con fracciones. Como ya hemos encontrado el punto, vamos a cambiar las unidades, de forma que A sigue siendo el (0, 0), B es el punto (17, 0), C es el (17, 17) y nuestro punto E tendría las coordenadas (x, y) = (1 + 3raíz(2), 5raíz(2) – 4), que son las que he puesto en el dibujo. Podríamos comprobar que las distancias cumplen lo que se nos pide, pero ahora vamos a calcular el ángulo AEB.

Si habéis estudiado geometría analítica, sabréis que para calcular el coseno de un ángulo podemos multiplicar escalarmente los vectores EA y EB, y dividir por su módulo.

Esto significa que hay que calcular (–x, – y)·(17 – x, – y) y dividirlo entre el producto de las raíces de x² + y² y de (17 – x)² + y². Podríamos trabajar todo el rato con el producto al cuadrado hasta el final, pero no va a hacer falta, porque ambos valores son muy similares.

El producto de los vectores (–x, – y)·(17 – x, – y) = x² – 17 x + y². En el caso que nos ocupa, da 1 + 18 + 6raíz(2) + 50 + 16 – 40raíz(2) – 17 – 51raíz(2) = 68 – 85raíz(2).

Ahora, la distancia al cuadrado x² + y² da 1 + 18 + 6raíz(2) + 50 + 16 – 40raíz(2) = 85 – 34raíz(2), y la distancia al cuadrado (17 – x)² + y² debe dar exactamente el cuádruple. Podemos comprobar que, en efecto, 256 + 18 – 96raíz(2) + 50 + 16 – 40raíz(2) = 340 – 136raíz(2) = 4*(85 – 34raíz(2).

Entonces, si multiplicamos la distancias d y 4d antes de sacar las raíces, tenemos 4d², y la raíz cuadrada, es decir, el producto del denominador de nuestra fracción es 2d, es decir, 170 – 68raíz(2).

Simplificamos el factor 17, que ha aparecido en las dos expresiones, y tenemos que el coseno que buscamos es (4 – 5raíz(2))/(10 – 4raíz(2)). Si racionalizamos esta expresión, obtenemos un valor mucho más familiar.

(4 – 5raíz(2))/(10 – 4raíz(2)) = (4 – 5raíz(2))(10 + 4raíz(2))/((10 – 4raíz(2))(10 + 4raíz(2))) = (40 – 40 – 50raíz(2) + 16 raíz(2))/(100 – 32) = – 34raíz(2)/68 = –raíz(2)/2

Es decir, que el ángulo que buscamos es exactamente 135º, es decir, 90 + 45º.