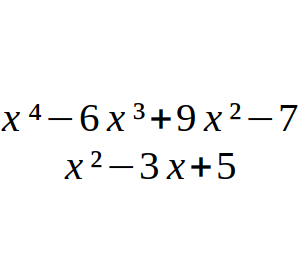Problema 1 del nivel B fase autonómica de la Olimpiada de la Comunidad Valenciana 2019
Se dirige a una edad de: 14-15 años
Sabiendo que el valor numérico del polinomio p(x) = x² – 3x + 5 en el punto x = k es 0, calcula el valor que tendrá q(x) = x⁴ – 6x³ + 9x² – 7 en el punto x = k.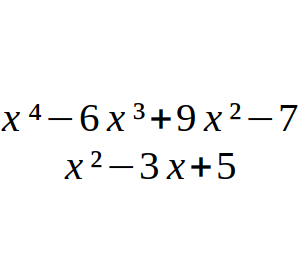
Solución:
Este problema consistía realmente en calcular el valor del polinomio q sin conocer el valor de k.
Si buscamos el valor de k, nos encontraremos que no es un número real (según nuestros conocimientos, no existirá) y en ese caso, puede que caigamos en la tentación de dar el problema por cerrado. Sin embargo, a pesar de no ser un número real, se puede evaluar el polinomio q a partir de propiedades como que p(k) = 0, en este caso.
La clave es ver si el polinomio p está contenido en el polinomio q un determinado número de veces, y para eso la herramienta que debemos usar es la división:
Si dividimos q(x) = x⁴ – 6x³ + 9x² – 7 entre p(x) = x² – 3x + 5, veremos que realmente x⁴ – 6x³ + 9x² – 7 = (x² – 3x + 5)( x² – 3x – 5) + 18.
Eso quiere decir que, si k hace que p(k) valga cero, en realidad el producto que forma el primer sumando es cero, con lo que el polinomio q(k) realmente valdrá 18.
En este problema veo algunas cosas que resultan poco adecuadas para un concurso, ya que dependiendo de lo que la persona que se enfrenta a él sepa, puede tratar de hacer una cosa u otra, y además debe estar familiarizado con la operación de división entre polinomios para darle respuesta, ya que no se me ocurre ningún otro método para darle respuesta.