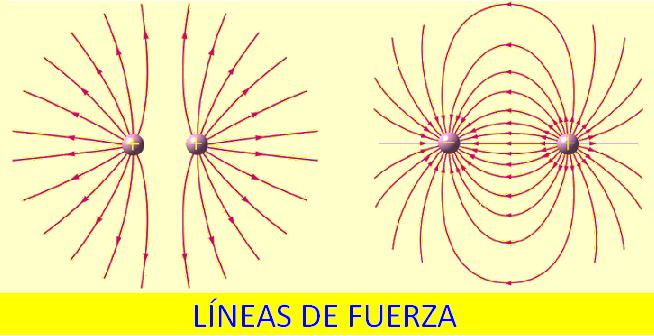
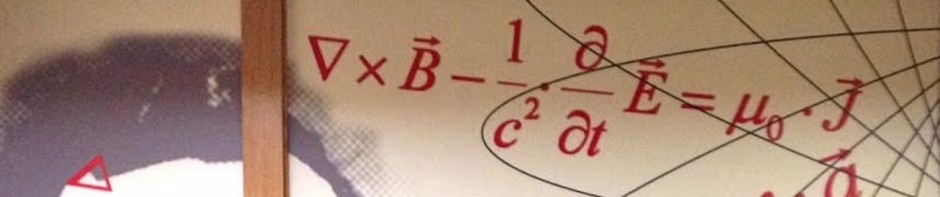Este tema está dedicado a la Electrostática, es decir, al estudio del campo y el potencial eléctricos originados por cargas eléctricas o distribuciones continuas de cargas en reposo. El tema comienza con el análisis de la electricidad con una breve discusión sobre el concepto de carga eléctrica y la naturaleza eléctrica de la materia, incidiendo especialmente en la conservación y cuantización de la carga, para pasar a la presentación de la ley de Coulomb, ley experimental que describe la fuerza entre dos carga eléctricas fijas puntuales. Posteriormente se introduce el concepto de campo eléctrico y se ve cómo puede describirse mediante líneas de campo o líneas de fuerza que tiene su origen en las cargas positivas y terminan en las cargas negativas, siendo el vector campo eléctrico tangente en cada punto a estas líneas de fuerza y su intensidad viene indicada por la densidad de las líneas de fuerza. El principio de superposición se deduce de la observación de que cada carga produce su propio campo eléctrico, independientemente de todas las otras cargas presentes a su alrededor, y que el campo resultante es la suma vectorial de los campos individuales. Aunque la carga está cuantizada, con frecuencia se presentan situaciones en las que un gran número de cargas están tan próximas que la carga total puede considerarse distribuida continuamente en el espacio, siendo necesario utilizar una densidad de carga para describir una distribución de un gran número de cargas discretas. Se introducen las densidades volumétrica, superficial y lineal de carga. En este contexto se muestran algunos ejemplos de cómo se calcula el campo eléctrico debido a diversos tipos de distribuciones continuas de carga (segmento rectilíneo, anillo y disco). Posteriormente se analiza el movimiento de cargas puntuales en campos eléctricos, en particular en campos uniformes, considerando las situaciones en las que la carga incide con una velocidad tanto paralela como perpendicular a la dirección del campo.
La fuerza eléctrica entre dos cargas puntuales está dirigida a lo largo de la línea que une las dos cargas y depende de la inversa del cuadrado de su separación, lo mismo que la fuerza gravitatoria entre dos masas. Como la fuerza gravitatoria la fuerza eléctrica entre cargas en reposo es conservativa y existe una función energía potencial asociada con la fuerza eléctrica, siendo la energía potencial proporcional a la carga. Se comprueba como la circulación del campo electrostático creado por una carga puntual a lo largo de una trayectoria cerrada es nula, lo que implica que el campo es conservativo. La energía potencial por unidad de carga se denomina potencial eléctrico, y a kontinuación se obtiene el potencial debido tanto a una carga puntual como a diversas distribuciones continuas de carga. Conviene destacar que sólo es posible determinar diferencias entre los potenciales en dos puntos diferentes. No se puede hablar, por tanto, de potencial absoluto en un punto del espacio, sino sólo de diferencia de potencial entre dos puntos. Si deseamos hablar de potencial eléctrico en un punto dado tenemos que tomar arbitrariamente, como valor de referencia, el potencial en un punto determinado. Normalmente es conveniente elegir como origen el potencial del infinito, pero es importante señalar que esto no siempre es posible, basta citar como ejemplos los casos de la línea infinita cargada o del plano cargado. A partir de la relación del campo eléctrico y el potencial se indica como se puede calcular uno de ellos si se conoce el otro. Conocido el campo eléctrico puede calcularse el potencial calculando la circulación del campo, es decir, mediante una integral. Sin embargo, si el potencial eléctrico es el dato puede determinarse el campo eléctrico mediante el gradiente, es decir, derivando. Asimismo se introducen las superficies equipotenciales como aquellas superficies que tienen el mismo potencial en todos sus puntos. Por ejemplo, las superficies equipotenciales alrededor de una carga puntual son superficies esféricas concéntricas estando la carga situada en el centro de las mismas. Se comprueba como en cada punto de una superficie equipotencial el campo eléctrico es perpendicular a la superficie, esto es, las líneas del campo eléctrico son perpendiculares a las superficies equipotenciales. A continuación se introduce el concepto de flujo del campo eléctrico y se discute la ley de Gauss que relaciona el campo eléctrico que existe en los puntos de una superficie cerrada con la carga neta encerrada dentro de la misma. La ley de Gauss se deduce de la ley de Coulomb y es una de las cuatro ecuaciones de Maxwell del Electromagnetismo. Esta ley proporciona un método práctico para el cálculo del campo eléctrico correspondiente a distribuciones de carga sencillas que posean una cierta simetría (esferas, cilindros, líneas, planos, etc.), haciendo uso del concepto de superficie gaussiana.