Capítulo 5 “Tablas de verdad y Contraejemplo”

En la lógica de primer orden el significado semántico que tiene una proposición se conoce como el valor de verdad de dicha proposición, respetando siempre el principio de bivalencia que dice que una proposición atómica puede tomar uno de los dos valores de verdad verdadero o falso.

“El perro es el mejor amigo del hombre”.

Esta sentencia se formaliza mediante una sentencia R, y por lo tanto la sentencia puede ser verdadera (V) o falsa (F), independientemente de que conozcamos si es cierta o falsa la declaración de la sentencia.

Podemos interpretar ¬R = V  si, y solo si, R = F , esto es lo mismo que decir:

El perro no es el mejor amigo del hombre

El perro es el mejor amigo del hombre

Si decimos que la primera es verdadera la otra tiene que ser falsa y viceversa

Tipos de interpretaciones:

– Interpretación modelo: Una interpretación I es un modelo de una fbf: A si bajo la interpretación I la fórmula A se interpreta como verdadera

– Interpretación contraejemplo: Una interpretación I es un contramodelo de una fórmula A si bajo la interpretación I la fbf: A se interpreta como falsa

Ejemplo “Paco canta y Mariano baila” A^B

A = “Paco canta”
B= “Mariano baila”

NOTA: En una conjunción de A + B ambas deben ser verdaderas, en cualquier otro caso el resultado es falso.

Si interpretamos que A y B son verdaderas obtenemos el valor de verdadero (I.Modelo)
Si interpretamos que A es falsa aunque B sea verdadera obtenemos el valor de falso (I.Contraejemplo)

Una tabla de verdad es una tabla que muestra el valor semántico de una fbf molecular para cada combinación de valores de verdad. Antes de hacer la tabla de verdad de una fbf se debe analizar dicha fbf encontrando todas las subfórmulas contenidas en ellas.

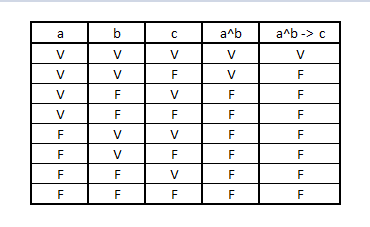
Usaremos el siguiente ejemplo: a^b -> c

A =	George estudia
B =	George aprueba examen
C =	George aprueba M1

Creamos una columna por cada variable que posee la fórmula, a continuación las que proposiciones moleculares en moléculas y atómicas, por último toda la regla original

Para añadir las filas deberemos contar el número de variables en este caso 3, eleveamos 2 al cubo en este caso, ya que hay 3 variables y nos da 8, ése es el número de filas que tendremos

Un contraejemplo para un razonamiento es la existencia de una interpretación que asigne valores verdaderos a las premisas y falso a la conclusión como es el caso de la fila 2 las premisas son verdaderas pero la conclusión falsa