| Un grafo no dirigido posee:
– Conjunto de vértices |
Un grafo dirigido posee:
– Conjunto de vértices |

Un grafo no dirigido asociado consiste en obtener los vértices y arcos de un grafo dirigido e ignorar la dirección de los arcos, convirtiendolos en arístas.
Un grafo mixto es aquel grafo que contiene tanto arcos como arístas.
A la hora de representar el contenido de un grafo, ya sea dirigido o no, diremos que un grafo X tiene un conjunto de vértices V y un conjunto de arcos/aristas A, por lo tanto lo expresaremos:
X =(V,A)
A continuación describiremos el conjunto V con los vértices que existen en el grafo.
V = {1,2,3}
Y por último si es un grafo dirigdo los arcos han de ir ordenados del siguiente modo arco = {VSaliente, VEntrante}, si no es dirigido no importa el orden de las aristas.
A={e1={2,1},…}
Grafo G Grafo H
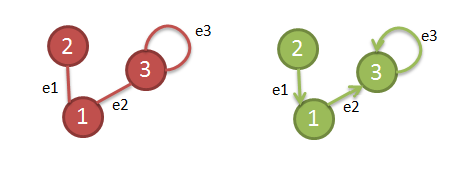
|
G = (V,A) V = {1,2,3} A = { e1 ={2,1}, e3 ={3,3}, e2 ={1,3} } ARISTAS NO ORDENADAS |
H = (V,A)
V = {1,2,3} A = { e1 ={2,1}, e2 ={1,3}, e3 ={3,3} } ARCOS ORDENADOS |
Los vértices origen y destino de una arista o arco son incidentes con la arista o arco.
Ejemplo: El vértice 2 es incidente con la arista/arco e1
Ejemplo: El vértice 1 es incidente con las aristas/arcos e1 y e2
Los dos vértices que son incidentes con una misma arista/arco se dice que son adyacentes.
Ejemplo: El vértice 1 y 2 son adyacentes.
Ejemplo: El vértice 1 y 3 son adyacentes.
Cualquier arista/arcos cuyos extremos sean el mismo vértice se llaman bucles.
Ejemplo: La arista/arco e3 tiene los extremos en el vértice 3, por lo tanto es un bucle.
Comments
One response to “Capítulo 7 “Conceptos Básicos sobre Grafos””
This is a very informative article. It really sparked my interest on several points. I agree with most of the points and am currently pondering the rest. Thank you for keeping your information so engaging.