La matriz de adyacencia de un grafo X y el número de sus vértices Y, al margen de que sea dirigido o no, será una matriz de YxY. en el caso de que tengamos un grafo con los vertices {A,B,C,D}, dibujaremos una tabla de 4×4 opcionalmente podemos señalizar las columnas y las filas con el nombre del vértice, por ejemplo:
NOTA: Recordemos que si existe algun arco/arista cuyos extremos sean iguales se llama bucle.
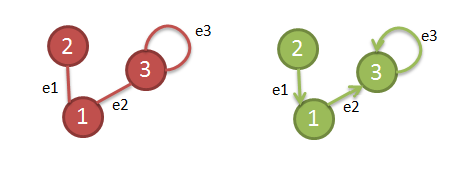
Grafo A |
Grafo B |
 |
|
La matriz de adyacencia para el Grafo A:
Iremos comprobando cada elemento de la matriz Aij (i=Fila j=Columna)
A11 ¿arista del v1 al v1? Si existiese pondriamos 2 ya que sería un bucle pero como no es el caso 0.
A12 ¿arista del v1 al v2? Si, ¿cuantas? 1
A13 ¿arista del v1 al v3? Si, ¿cuantas? 1
Y así lo harémos con cada fila y con cada columna quedando la matriz así:
| 0 1 1 |
| 1 0 0 |
| 1 0 2 |Al tratarse de un grafo no dirigido obtenemos una matriz simétrica, por lo que si susamos cada fila o cada columna obtendremos el grado de cada vértice.
La matriz de adyacencia para el Grafo B:
Se comprueba exactamente igual que la otra, con la diferencia que los arcos tienen una dirección.
El resultado es:
| 0 0 1 |
| 1 0 0 |
| 0 0 1 |Al tratarse de un grafo dirigido si sumamos las columnas obtenemos el grado de entrada y si sumamos las filas el grado de salida .
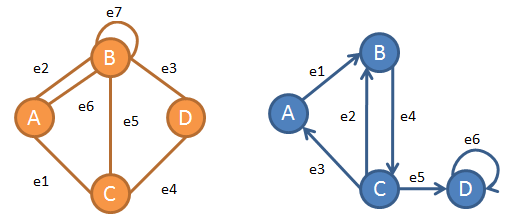
Ejemplo
 |
|
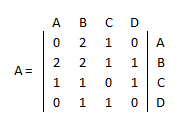 |
 |
Comments
One response to “Capítulo 10 “Matriz de Adyacencia””
Tks…
This information really helped me, I am sharing with a few friends….