El algoritmo de fleury encuentra un tour o camino euleriano en un grafo no dirigido, sabiendo si existen por el siguiente teorema:
Teorema 1
Sea G un grafo no dirigido y conexo
– G es euleriano si y sólo si no tiene vértices de grado impar.
– G contiene un camino euleriano si y sólo si tiene exactamente dos vértices de grado impar.
Ejemplo
 |
 |
 |
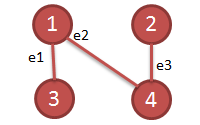
| Tiene dos vértices de grado impar por lo tanto no es un grafo euleriano pero si tiene un camino euleriano:
v2 e3 v4 e2 v1 e1 v3 |
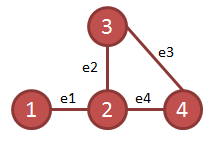
Tiene dos vértices de grado impar por lo tanto no es un grafo euleriano pero tiene un camino euleriano:
v2 e2 v3 e3 v4 e4 v2 e1 v1 |
Si es un grafo euleriano |
Ahora que sabemos que el grafo tres es euleriano debemos seguir los siguientes pasos:
Paso 1:
– Nos creamos una cadena dónde iremos guardando nuestro tour euleriano
T = {}

Paso 2:
– Seleccionamos un vértice x.
– Seleccionamos una arista incidente a x, que no desconecte el grafo si la quitamos.
– Añadimos la arista a nuestra cadena y la quitamos del grafo
– Si x no tiene más aristas incidentes lo quitamos.
T = {e3 }
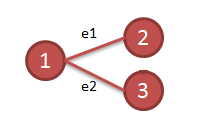
Repetimos el paso 2
T = {e3 e2}
Como el vértice 3 se queda sin aristas lo quitamos.
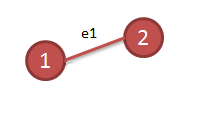
Repetimos el paso 2
T = {e3 e2 e1}
Como el vértice 1 se queda sin aristas lo quitamos.

No hay más aristas ya tenemos nuestro tour euleriano.
NOTA: Deben aparecer todas las aristas en el tour/camino