Un Tour de G: una cadena cerrada que atraviesa cada arista de G al menos una vez.
Un Tour euleriano de G: una cadena cerrada que atraviesa cada arista exactamente una vez.
Un Grafo euleriano es aquel en el que podemos encontrar un tour euleriano.
Un Camino euleriano es una cadena o cadena simple que atraviesa cada arista exactamente una vez.
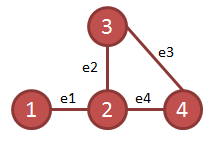
Grafo A
|
Grafo Euleriano: No
Tour: v1 e1 v2 e2 v3 e3 v4 e4 v2 e1 v1 Tour Euleriano: No tiene, porque tiene vértices de grado impar Camino Euleriano: v1 e1 v2 e2 v3 e3 v4 e4 v2 |
Grafo B
|
Grafo Euleriano: Si Tour: v2 e1 v1 e2 v3 e3 v2 Tour Euleriano: v1 e1 v2 e3 v3 e2 v1 Camino Euleriano:v1 e1 v2 e3 v3 e2 v1 |
Teorema
Sea G un grafo no dirigido y conexo
– G es euleriano si y sólo si no tiene vértices de grado impar.
– G contiene un camino euleriano si y sólo si tiene exactamente dos vértices de grado impar.
Sea G un grafo dirigido y débilmente conexo
– Si y sólo si para todo vértice su grado de entrada es igual a su grado se salida.

Comments
One response to “Capítulo 13 “Leonardo Euler””
of course like your web-site but you need to take a look at the spelling on quite a few of your posts. Many of them are rife with spelling issues and I find it very troublesome to inform the truth nevertheless I¡¦ll definitely come again again.