Tema 5: Fundamentos de los Grafos
Ficha de Aprendizaje del Tema 5
Fundamentos de los Grafos – Introducción a los Grafos
- Respuestas (breves) a las siguientes preguntas:
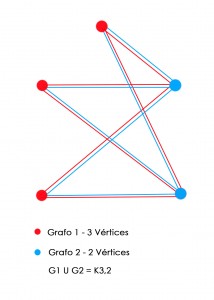
- ¿Qué significa que un grafo sea K3, 2?
Un Grafo K3, 2 es un grafo no dirigido, completo, simple y bipartido en la que el grafo G es la unión del Grafo1 y Grafo2: G = G1 U G2.
Llamamos Kn al grafo completo no dirigido y simple con n vértices. Llamamos Km/n al grafo no dirigido, completo, simple y bipartido resultante de la unión de un grafo (G1) con m vértices con un grafo (G2) de n vértices unidos, es decir, el 3 es el número de vértices de G1 unidos al G2 con sus 2 vértices: K3, 2
2. Explica que es un grafo bipartido y bipartido completo.
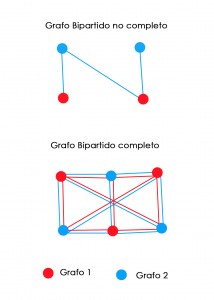
Un grafo Bipartido es un grafo en el que hay una partición (G1, G2) del conjunto de vértices de forma que toda arista tiene un extremo en G1 y otro en G2, es decir, el grafo se puede dividir en dos (G = G1 U G2) y está formado por 2 conjuntos de vértices en común (uno de cada grafo) y ninguno o casi todos son disconjuntos (mínimo uno conjunto); sus aristas/ arcos conectan ambos grafos. No puede haber bucles.
Nota: un grafo dirigido es bipartido si su grafo no dirigido asociado lo es.
Un grafo Bipartido Completo es un grafo formado por la unión de dos grafos (G = G1 U G2) en el que cada vértice de G1 está unido con cada vértice de G2, es decir, todos los vértices de G1 tienen que estar conectados con G2. No puede haber bucles.
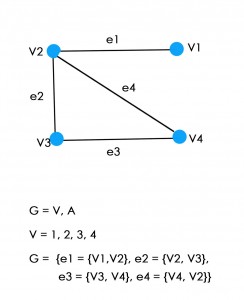
3. Representa gráfica y matemáticamente un grafo no dirigido conexo con al menos 4 vértices.
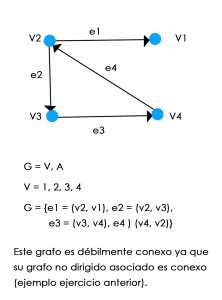
4. Representa gráfica y matemáticamente un grafo dirigido que no sea conexo pero que sea débilmente conexo.
5. Escribe una condición necesaria para que un grafo sea conexo.
Para que un grafo sea conexo es necesario que dicho grafo no se pueda dividir en subgrafos y que sus componentes conexas sea igual a 1, es decir, que haya una cadena que conecte todos con todos, empezando por cualquiera de sus vértices.
Nota: todo par de vértices están conectados.
6. ¿Cómo calcularías el grado de un vértice de un grafo dirigido a partir de la matriz de adyacencia?
En caso de ser un grafo dirigido, cada vértice que lo compone tiene tanto grado de salida como de entrada, necesitaremos de la matriz de adyacencia.
Teniendo la matriz de adyacencia, sumaremos todos los 0 y 1 de la fila o columna de ese vértice, si es el vértice V1 sumaremos todos los elementos de la fila 1, hallando así el grado de salida; si sumamos los elementos de la columna 1 encontraremos los de entrada.