Tema 6: Accesibilidad y Conectividad
Ficha de Aprendizaje del Tema 6
Fundamentos de los Grafos – Accesibilidad y Conectividad
- Respuestas (breves) a las siguientes preguntas:
1. ¿Qué significa que un vértice de un grado alcance a otro vértice del grafo?
Significa que el vértice es accesible a otro vértice del grafo, sea o no a sí mismo, es decir, otro vértice puede acceder a ese vértice mediante una arista (sea dirigida o no). Esto se puede ver claramente en la matriz de accesibilidad, donde 1 significa que alcanza y 0 que no alcanza.
Por ejemplo: si en la fila de V1 (vértice 1 de salida) hay un 1 bajo V1 (vértice 1 de entrada) significa que V1 alcanza a V1, por tanto, en este caso, es un bucle.
2. ¿Cuántas matrices Rj aparecen en la sucesión del algoritmo de Warshall para calcular la matriz de accesibilidad R de un grafo de 5 vértices?
Dado que en el algoritmo de Warshall debe ir de R0 hasta Rn, donde n es el número de vértices del algoritmo, en esta caso, n = 5 por lo que Rn = R5; y donde R0 es la matriz de adyacencia (modificada para que no todos sus elementos sean 0, sino 1). Las matrices que se calculan desde R0 a R5 son matrices que permiten llegar a R5.
Teniendo R5 debemos transformar en 1 los elementos de la diagonal ya que, por convenio, todo vértice es alcanzado por él mismo por un camino de longitud 0.
Nota: para grafos no dirigidos es R = Q donde R es la matriz R0 (matriz de adyacencia) y Q la matriz de accesibilidad. Ambas, en este caso, son iguales.
3. Escribe una condición necesaria para que un grafo sea conexo.
Para que un grafo sea conexo es necesario que sus componentes conexas valgan 1, lo que significa que dicho grafo no puede estar dividido en subgrafos porque hay una cadena que conecta todos con todos, es decir, todos son alcanzados por todos con los que mediante desde cualquier vértice puedes llegar a cualquier otro.
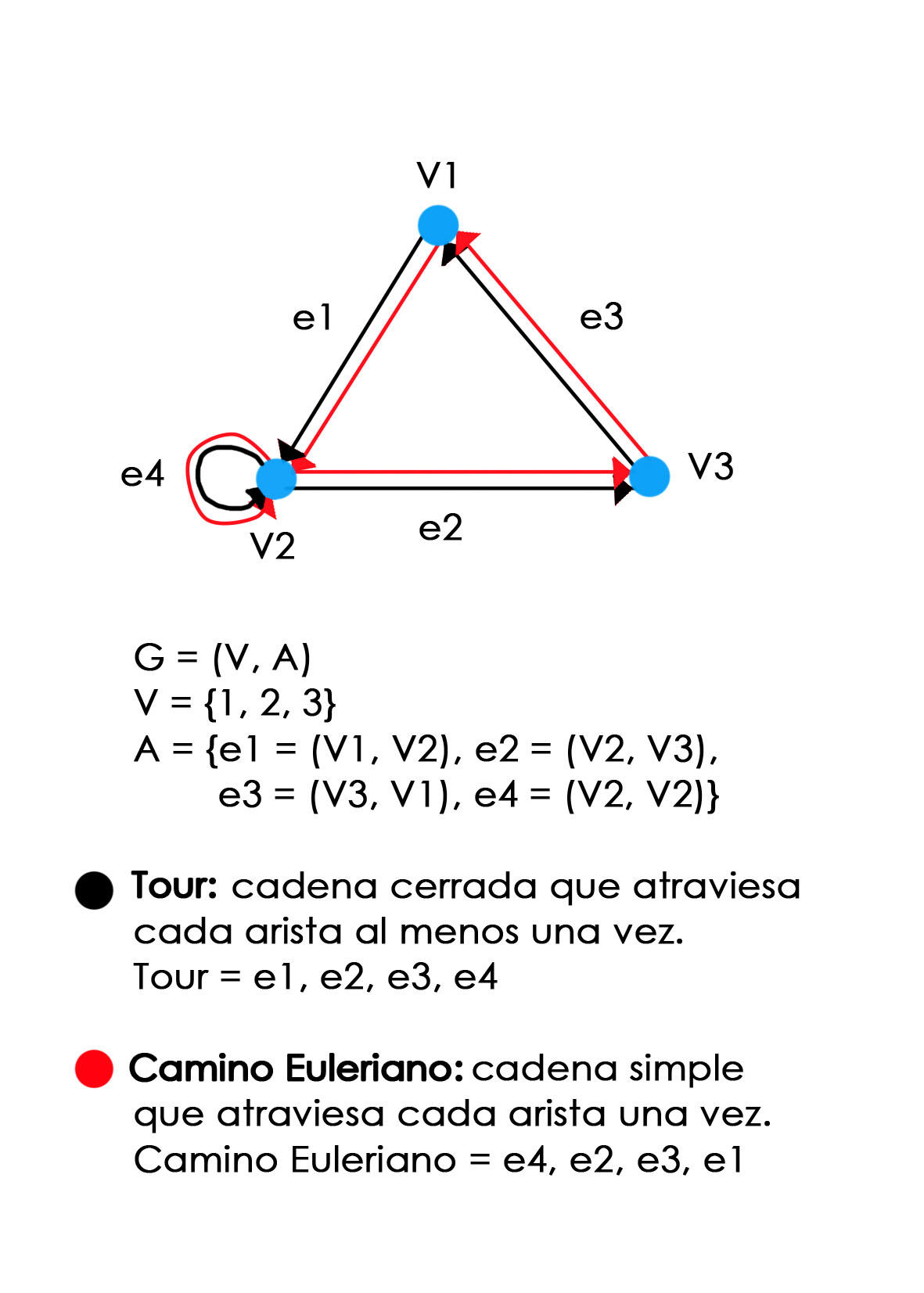
4. Representa gráfica y matemáticamente un grafo dirigido no simple que tenga y tour y un camino euleriano.
5. Si G es un grafo no dirigido con unos vértices de grado par y otros de grado impar. ¿Cuándo podemos asegurar que G tiene un camino euleriano?
Para que el grafo G tenga un camino euleriano tiene que tener 2 vértices de grado impar y que sea una grafo conexo.