En este post vamos a ver como podemos representar un grafo mediante matrices de adyacencia e incidencia.
MATRIZ DE ADYACENCIA
Definición
Sea G un grafo con n vértices {vi}i –> n = 1. Llamamos matriz de adyacencia a la matriz de orden n x n, de manera que cada elemento de la matriz es igual al numero de aristas|arcos del vértice i al j, es decir los caminos de longitud igual a la potencia de la matriz A = {aij}. Si A2, entonces los elementos de esta matriz contendrán el numero de caminos de longitud 2 entre cada vértice.
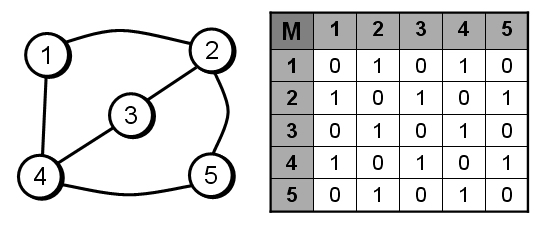Ejemplo: Para el vértice 1, vemos que es adyacente con el 2 y el 4, en su matriz A.
De modo de que cumplen las siguientes propiedades:
1. Sea G un grafo no dirigido con matriz de Adyacencia A. Entonces, la suma de los elementos de cada fila, es igual al grado ese vértice.
2. En el caso de los grafos dirigidos, la suma en cada fila nos la el grado de salida, y el de cada columna el grado de entrada de cada vértice.
3. Sea G un grafo con matriz de adyacencia A. Entonces, el elemento (i,j) de la matriz Ar, siendo r >= 1, es igual al numero de cadenas, de longitud r, del vértice vi al vértice vj.
MATRIZ DE INCIDENCIA
Definición
Sea G = {V,A} un grafo no dirigido con n vértices y m aristas siendo V = {vi}i –> n = 1, y A = {ai}i –> m = 1. Llamamos matriz de incidencia de G a la matriz de orden nxm compuesta de los siguientes elementos:
M = [mij] / mij =>
0 si el vértice i no es incidente con la arista j.
1 si el vértice i es incidente con la artista j.
2 si la arista j es un bucle en el vértice i.
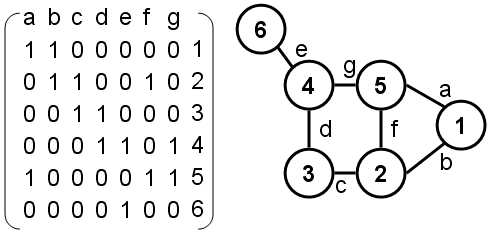
Vamos a verlo mas claro con un ejemplo:
En las filas tenemos los vértices del grafo (numerados a la derecha), y en las columnas podemos ver las aristas de este.
Si cogemos, por ejemplo, el vértice 5 (fila 5), vemos que en la columnas a, f y g tiene un 1, esto quiere decir, que el vértice 5 es incidente con las aristas a, f y g, en el caso de los bucles se contarían como 2.
Para el caso de los grafos dirigidos es diferente, ya que hay vértices iniciales y finales para cada arco. Quedaría de la siguiente manera:
B = [bij] / bij =>
0 si el vértice i no es incidente con el arco j.
1 si el vértice i es el inicial del arco j.
-1 si el vértice i es el final del arco j.
2 si el arco j es un bucle en el vértice i.
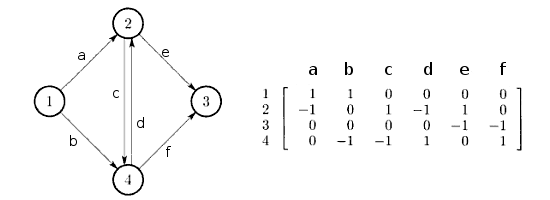
Veamos un ejemplo:
Para el arco a (primera columna), el vértice inicial es el 1 (fila 1) y el final el 2 (fila 2). Si lo miramos desde los vértices (filas), por ejemplo, del vértice 2 salen los arcos c y e (1), y llegan los arcos a y d (-1).
Para las matrices de incidencia también se cumplen una serie de propiedades:
1. Si el grafo G es no dirigido. La suma de los elementos de cada fila de la matriz de incidencia es igual al grado del correspondiente vértice.
2. Si el grafo G es no dirigido. La suma de los elementos de cada columna de la matriz de incidencia debe ser igual a 2. Es lógico, cada arista tiene un vértice en cada extremo, dos en total, no puede tener mas.
3. Si el grafo G es dirigido y sin bucles. La suma de los elementos de cada columna de la matriz de incidencia es igual a 0. Ya que ponemos 1 para el vértice inicial y -1 para el final, y el arco solo incide con un vértice a cada uno de sus extremos, es decir, 2 vértices, por lo que 1-1=0.
TABLAS DE INCIDENCIA
1. Sea G un grafo no dirigido. Llamaremos tabla de aristas incidentes del grafo G a una tabla que lista, para cada vértice v, todas las aristas incidentes con v.
2. Sea G un grafo dirigido:
Llamaremos tabla de arcos salientes del grafo G a una tabla que lista, para cada vértice v, todos los arcos salientes de v.
Llamaremos tabla de arcos entrantes del grafo G a una tabla que lista, para cada vértice v, todos los arcos entrantes en v.