1. ¿Que significa que un grafo sea K3,2?
Que es un grafo V = V1 + V2, lo cual será un grafo no dirigido, bipartido, completo y simple.
V1 = 3 y V2 = 2.
2. Explica que es un grafo bipartido y bipartido completo.
Un grafo bipartido es un grafo cuyos vértices se pueden separar en dos conjuntos disjuntos V1 y V2 y las aristas siempre unen vértices de un conjunto con vértices de otro.
Un grafo bipartido completo es un bipartito en el que todos los vértices de la partición V1 están conectados a todos los vértices de la partición V2 y viceversa.
3. Representa gráfica y matemáticamente un grafo no dirigido conexo con al menos 4 vertices.
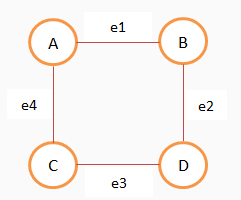
G = (V, A)
V = {A, B, C, D}
A = {e1 = {A, B}, e2 = {B, D}, e3 = {D, C}, e4 = {C, A}}
4. Representa gráfica y matemáticamente un grafo dirigido que no sea conexo pero que sea débilmente conexo
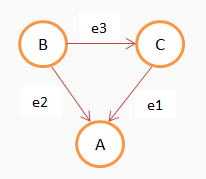
G = (V, A)
V = {A, B, C}
A = {e1 = (C, A), e2 = (B, A), e3 = (B, C)}
El grafo es débilmente conexo ya que su grafo no dirigido asociado es conexo.
5. Escribe una condición necesaria para que un grafo sea conexo
Un grafo es conexo si todo par de vértices está conectado, donde dos vértices están conectados si existe un camino de vértice a otro y viceversa.
6. ¿Cómo calcularías el grado de un vértice de un grafo dirigido a partir de la matriz de adyacencia?
Con las filas obtendremos los arcos de salida y con las columnas obtendremos los arcos de entrada. Las filas y las columnas deben ser las mismas, primera fila con primera columna, segunda fila con segunda columna y así sucesivamente. La suma de los arcos de salida con los arcos de entrada nos dará el grado del vértice. V = (V(ds)) + (V(de)).