GRAFOS PONDERADOS
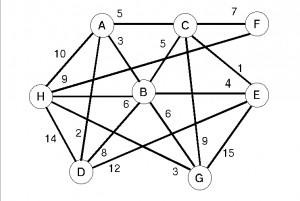
En muchos casos, es preciso atribuir a cada arista un número específico, llamado valuación, ponderación o coste según el contexto, y se obtiene así un grafo valuado o ponderado.
Por ejemplo, un representante comercial tiene que visitar n ciudades conectadas entre sí por carreteras; su interés previsible será minimizar la distancia recorrida (o el tiempo, si se pueden prever atascos). El grafo correspondiente tendrá como vértices las ciudades, como aristas las carreteras y la valuación será la distancia entre ellas.
Definiciones:
1. Un grafo simple G = (V, A) (grafo simple dirigido, respectivamente) diremos que es un grafo ponderado si tiene asociado una función W : A -> R llamada función de ponderación.
La imagen de cada arista (arco, respectivamente) determinada por los vértices vi y vj la llamaremos peso de la arista (b) y lo denotaremos por Wij.
2. Sea G = (V, A) un grafo ponderado finito tal que V = {v1, … , vn}. Llamaremos matriz de peso del grafo G a la siguiente matriz de orden n x n:
Es decir, que pondremos el valor del peso cuando lo tenga, y el símbolo infinito cuando no exista tal valor.
3. En un grafo ponderado llamamos peso de un camino a la suma de los pesos de las aristas (o arcos) que lo forman.
4. En un gafo ponderado llamamos camino mas corto entre dos vértices dados al camino de peso mínimo entre dichos vértices.
5. En un grafo ponderado llamaremos camino mas largo o camino critico entre dos vértices al camino de peso máximo entre dichos vértices.
CAMINOS MAS CORTOS: ECUACIONES DE BELLMAN
Vamos a suponer un grafo dirigido en el que los pesos asociados a los arcos son todos no negativos. Además que los vértices del grafo esta numerados de 1 a n, de forma que Wij representa el peso del arco (i, j) y que el vértice 1 es el origen del camino. Uj denotara el peso del camino mas corto del 1 a j.
Teorema:
Siendo el camino mas corto, de un grafo ponderado, de 1 a j pasando por k vértices, entonces las secciones de este camino son los caminos más cortos entres los respectivos vértices dentro del camino. Es decir, que un camino más corto de un vértice a otro esta formado por caminos más cortos entre cada vértice de esta sucesión.
Corolario:
Supongamos que en un grafo ponderado tenemos un camino más corto entre los vertices 1 y j. Sea k el vertice inmediatamente anterior a j en este camino. Entonces la seccion de este camino desde 1 a k es el c.m.c. entre estos dos vertices. Además el peso del c.m.c. de 1 a j (Uj) sera igual al peso del c.m.c. de 1 a k mas el peso de k a j.
Uj = Uk + Wkj
De aquí obtenemos las ecuaciones de Bellman, que nos permiten saber el peso del camino más corto desde el primer vértice al j, pudiendo ser j desde el vértice 2 al n.
U1 = 0
k distinto de j
Uj = mín{Uk + Wkj} j = 2, … , n
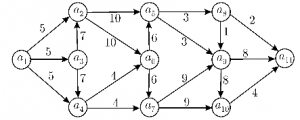
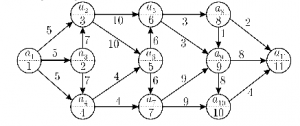
GRAFOS ACÍCLICOS: MÉTODO DEL CAMINO CRÍTICO (PERT).
Teorema:
El método PERT consiste en la representación gráfica de una red de tareas, que, cuando se colocan en una cadena, permiten alcanzar los objetivos de un proyecto.
Un grafo dirigido no tiene circuitos si y solo si existe una numeración de los vértices para la que se cumple que si (i, j) es un arco del grafo entonces i<j. Esto es el método PERT.
Con esta numeración, las ecuaciones de Bellman pueden ser reemplazadas por:
U1 = 0
k menor que j
Uj = mín{Uk + Wkj} j = 2, … , n
Pero antes de aplicar la ecuación, hay que numerar los vértices en el orden adecuado, para ello seguimos los siguiente pasos:
Etapa 1. Inicializar i<-i, V(1)= V
Etapa 2. Tomar v E V(i) tal que de(v)=0 en G[Vi].
Etapa 3. Numerar el vértice V como vértice 2
Hacer V(i+1) = V(1) – {V}
Hacer i<-i+1
Etapa 4. Si V(i) = ø
Aquí un ejemplo de un grafo antes y después de numerarlo, y las ecuaciones de Bellman aplicadas a este:
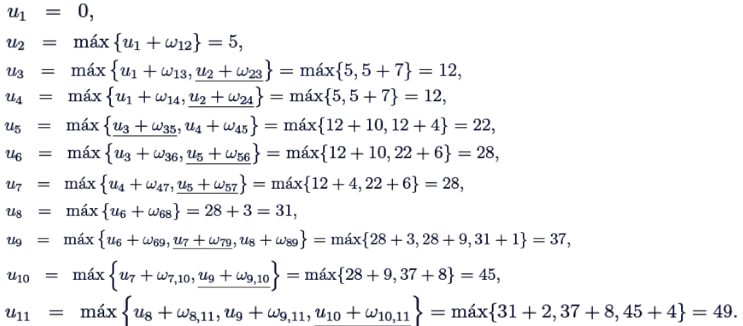
Hasta aquí llega la matemática discreta del año 2010-2011 de Ingeniería Multimedia. Espero que estos apuntes sean de ayuda a quien los necesite. Saludos.