El determinante de matrices de dimensión menor que 4 se calcula rápidamente mediante reglas o fórmulas. Para dimensiones mayores, es necesario desarrollar el determinante mediante otros métodos, como la regla de Laplace.
Dimensión 1×1
Una matriz de dimensión 1×1 tiene la forma
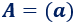
El determinante de A es el único elemento de la matriz:
Dimensión 2×2
Las matrices de dimensión 2×2 tienen la forma
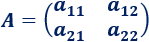
Su determinante es
Regla mnemotécnica: multiplicamos en las diagonales y las restamos.
Dimensión 3×3 (Regla de Sarrus)
Las matrices de dimensión 3×3 tienen la forma

Su determinante se calcula mediante la llamada regla de Sarrus:
Regla mnemotécnica: la regla de Sarrus parece complicada, pero si os fijáis bien, también estamos multiplicando diagonales.
Más información de matrices:
- Suma de matrices
- Multiplicar matrices (1)
- Multiplicar matrices (2)
- Eliminación de Gauss (1)
- Eliminación de Gauss (2)
- Determinantes de matrices (1)
- Determinantes de matrices (2)
- Matriz inversa (1)
- Matriz inversa (por Gauss) (2)
- Matriz inversa (por determinantes) (3)
- Ejemplos del teorema de Rouché-Frobenius (1)
- Demostración y ejemplos del teorema de Rouché-Frobenius (2)
- Ejemplos de la regla de Cramer (1)
- Ejemplos de la regla de Cramer (2)
- Ecuaciones matriciales (1)
- Ecuaciones matriciales (2)
- Potencias enésimas de matrices (1)
- Potencias de matrices (2)
- Problemas teóricos de matrices
- Propiedades de los determinantes
- Matriz adjunta
- Más temas de matrices
Calculadoras online de matrices:

