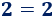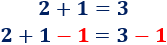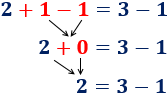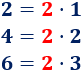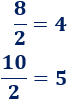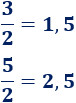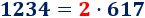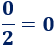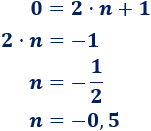Para ver que el número 0 es par, debemos recordar los conceptos y propiedades de los números pares y los números impares.
Número par
Los números pares son los números enteros que son múltiplos de 2, es decir, los números que se obtienen al multiplicar otro número por 2.
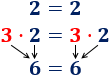
Ejemplo: el 2, el 4 y el 6 son pares porque
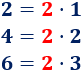
Los números pares también se definen como los números divisibles entre 2, es decir, como los números cuya división entre 2 tienen como resultado un número entero.
Ejemplos
- El 8 y el 10 son pares porque se obtiene un entero al dividirlos entre 2:
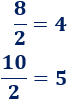
- El 3 y el 5 no son pares porque se obtienen decimales al dividirlos entre 2:
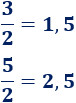
Propiedad
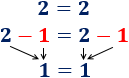
Si un número a es par, existe algún número entero n tal que

Ejemplos
- El número 1234 es par y se puede escribir como
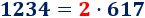
- El número 1010 es par y se puede escribir como

Número impar
Los números impares son los números enteros que no son pares.
Ejemplos
Como 1, 3 y 5 no son divisibles entre 2 (el resultado no es un número entero), son números impares.
Propiedad
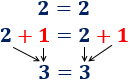
Si un número a es impar, entonces existe algún número entero n tal que

Ejemplos
- El número 123 es impar y se puede escribir como

- El número 101 es impar y se puede escribir como

El número 0 es par
El número 0 es par porque es múltiplo de 2:

Además, la división 0 entre 2 es un número entero:
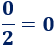
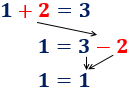
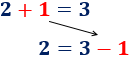
Además, si 0 fuese un número impar, debería existir un número entero n tal que

Pero, si resolvemos la ecuación anterior, tenemos que n ha de ser un número no entero:
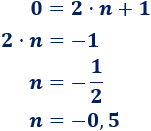
Más información y temas relacionados: