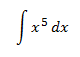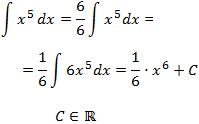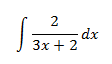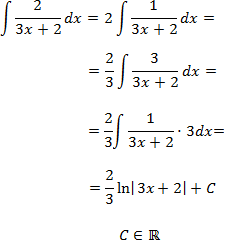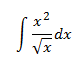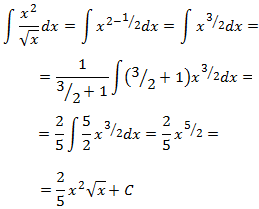Las integrales inmediatas o directas son las integrales que no requieren aplicar ningún método de integración porque son muy sencillas. Por ejemplo, la integral de 2x es x2 + C, donde C es la constante de integración.
A veces, el integrando es una función multiplicada por su derivada. En este caso, la integral es la propia función:
∫f(x)·f'(x)dx = f(x) + C
No olvidéis escribir siempre la constante de integración C.
Veamos algunos ejemplos de integrales inmediatas.
Integral 1
Integral de la potencia x a la quinta:
Aplicaremos la propiedad “una constante puede entrar o salir de la integral”.
Sólo falta un 6 multiplicando para tener la derivada de x6. Multiplicamos y dividimos por 6 la integral para introducir un 6 en la integral:
Integral 2
Integral de una función racional:
Normalmente, las integrales inmediatas de funciones racionales son la derivada de un logaritmo. Si no es así, tendremos que aplicar otros métodos para integrales de funciones racionales.
El integrando será la derivada de un logaritmo si conseguimos escribir el numerador como la derivada del denominador. Para ello, en esta integral, debemos cambiar el 2 por un 3:
Integral 3
Integral de un cociente con una raíz cuadrada en el denominador:
Vamos a escribir la raíz cuadrada en forma de potencia. De este modo, aplicando las propiedades de las potencias, el integrando será muy simple (una potencia).
Más integrales resueltas: