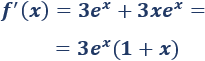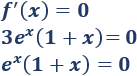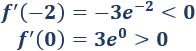Máximos y mínimos

Extremos relativos

Un punto a es un máximo relativo de la función f si f(a)≥f(x) para los x cercanos a a. Es un mínimo relativo si f(a)≤f(x).

Ejemplo:

Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

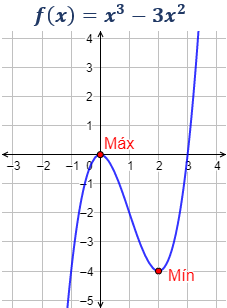
La función tiene un máximo relativo en (0, 0) y un mínimo relativo en (2, -4).

Observad que x=0 es un máximo en los puntos de su alrededor, pero no en todos, ya que, por ejemplo,

Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

Extremos absolutos

Si a es un mínimo (o un máximo) para todo x del dominio de f, se dice que es un mínimo absoluto (o un máximo absoluto).

Es decir,

  • a es un mínimo absoluto de f si

Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

  • a es un máximo absoluto de f si

    Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

  • a es un extremo absoluto de f si es un mínimo absoluto o un máximo absoluto.

Nota: observad que un extremo absoluto cumple la definición de extremo relativo.

Ejemplo:

Los extremos de la función del ejemplo anterior no son absolutos.

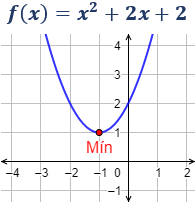
El vértice de una parábola siempre es un extremo absoluto. Por ejemplo, la siguiente parábola tiene un mínimo relativo en (-1, 1):

Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

Regla de la primera derivada

Si f es derivable en el intervalo I=(a, b), entonces

  • f es creciente en I si

    Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

  • f es decreciente en I si

    Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

Por tanto, los candidatos para ser extremos son los puntos que anulan la derivada.

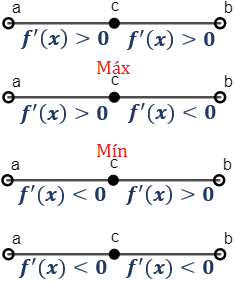
Supongamos que f es derivable en I=(a, b),  que c∈I es un punto crítico (es decir, f'(c)=0). Entonces, pueden darse las siguientes situaciones (estudio del signo de la derivada en los intervalos (a, c) y (c, b)):

Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

Es decir, c es un máximo si la función es f es creciente a su izquierda y decreciente a su derecha. Y es un mínimo si f es decreciente a su izquierda y creciente a su derecha.

Para saber si f’ es positiva o negativa un intervalo, sólo tenemos que ver el signo de f'(x) de cualquier x de dicho intervalo.

Ejemplo:

Vamos a calcular los extremos de la función

Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

La primera derivada es

Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

Igualamos a 0 y resolvemos la ecuación para hallar los puntos críticos:

Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

La función ex nunca es igual a 0. Por tanto, el único punto crítico es x=-1.

El punto crítico divide los reales en dos intervalos:

Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

Evaluamos la derivada f’ en un punto arbitrario de cada uno de los intervalos para saber si f es creciente o decreciente:

Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

Por tanto, f es monótona decreciente en el intervalo (-∞, -1) y monótona creciente en (-1, +∞).

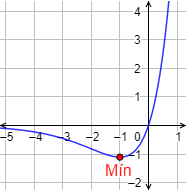
Como consecuencia, x=-1 es un mínimo. Además, por la monotonía de la función, se deduce que es un mínimo absoluto.

Gráfica:

Definimos extremos relativos y absolutos de una función y enunciamos las reglas de la primera y segunda derivada. Proporcionamos ejemplos y resolvemos algunos problemas. Bachillerato y universidad. Análisis de una variable. Matemáticas.

 

Enlaces con problemas de funciones: