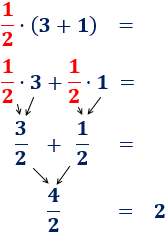
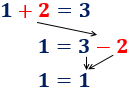
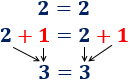
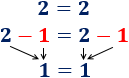
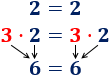
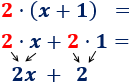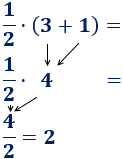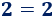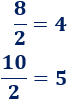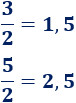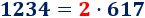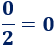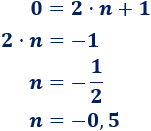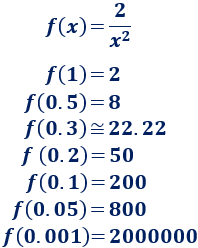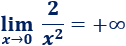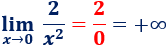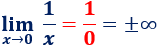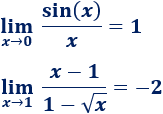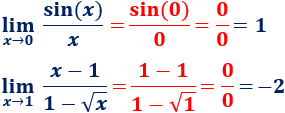Es frecuente escuchar a gente decir que el resultado de dividir entre 0 es infinito. Sin embargo, esto no es correcto: no se puede dividir entre 0 y, en los supuestos casos en que “se puede”, el resultado no sería siempre infinito. A continuación, mostramos explicamos el por qué y el origen de este falso mito.
Se dice que el resultado es infinito porque cuanto más se acerca el divisor a 0, más grande es el resultado de la división. Por ejemplo,
- 1 entre 2 es 0,5
- 1 entre 1 es 1
- 1 entre 0,5 es 2
- 1 entre 0,3 es 3,3333…
- 1 entre 0,1 es 10
- 1 entre 0,01 es 100
- 1 entre 0,001 es 1.000
- 1 entre 0,0001 es 10.000
En el cálculo diferencial, dada una función y = f(x), el límite de dicha función en el punto x = a se denota por

Y puede verse como el número al que se aproxima la función y = f(x) cuando x se aproxima a x = a.
Por ejemplo, consideremos la función f(x) = 2/x² cuya gráfica es la siguiente:
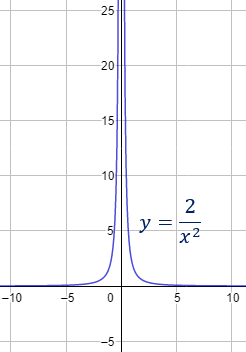
Observando la gráfica se aprecia claramente que cuando x se aproxima a 0 los valores y = f(x) crecen mucho. Por ejemplo,
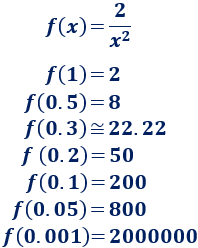
La función y = f(x) crece infinitamente cuando x se aproxima a 0, por lo que se dice que la función tiene límite infinito:
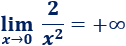
El cálculo de límites a veces resulta un poco complicado, razón por la que se utilizan ciertas reglas que SÓLO tienen sentido cuando trabajamos con límites. Una de estas reglas es que un número distinto de 0 dividido entre 0 es infinito. Por ejemplo, usamos esta regla para calcular el límite anterior:
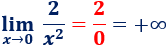
Nota: técnicamente, la igualdad anterior no es correcta (por eso se escribe en rojo).
Veamos otro ejemplo:
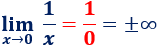
Es importante remarcar que esta regla exige que sea un número DISTINTO de 0 dividido entre 0, ya que 0/0 es una indeterminación (indeterminación 0/0) que en cada límite puede tener un resultado distinto.
Por ejemplo,
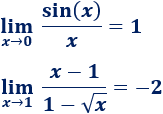
Y, sin embargo, si sustituimos x = 0 en los límites, tenemos la fracción 0/0:
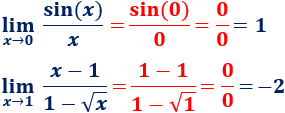
Conclusión
Como conclusión, el resultado de dividir entre cero no es infinito. De hecho, ni siquiera está permitida la operación “dividido entre 0”, como hemos visto. Ahora bien, en el cálculo diferencial se utiliza la regla “un número entre 0 es infinito” sólo para referirse a que el resultado de dividir entre números cercanos a cero es un número muy grande.
Más ejemplos y temas relacionados: