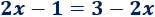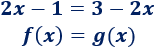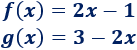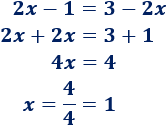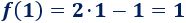Observando la gráfica de una parábola podemos obtener la siguiente información:
- Las coordenadas del vértice.
- Las coordenadas de 3 puntos distintos de la gráfica.
- Los puntos de corte con el eje abscisas.
Esta información es suficiente para hallar la ecuación de una parábola, la cual tiene la forma
siendo a ≠ 0.
Ahora, recordamos algunos conceptos que nos ayudarán a obtener los coeficientes a, b y c a partir de la gráfica de la parábola.
Vértice
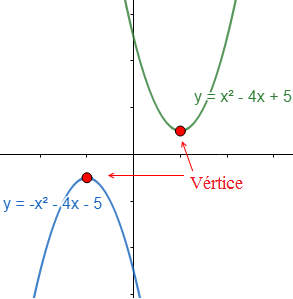
Todas las parábolas tienen forma de ∪ (si a>0) o de ∩ (si a<0). En cualquier caso, el punto más alto o máximo (si a>0) o el punto más bajo o mínimo (si a<0) de la parábola es el punto cuya primera coordenada es
Ejemplo de una parábola con forma de ∪ (verde) y otra con forma de ∩ (azul):
Raíces
Los puntos (α, 0) de la parábola cortan al eje de abscisas. Una parábola puede tener 1, 2 o ningún punto de corte con este eje. Se pueden dar 3 casos.
Caso 1:
La parábola tiene dos raíces (reales) distintas: α y β. Entonces, se cumple la siguiente igualdad:
Caso 2:
La parábola tiene una única raíz (real): α. Entonces, se cumple que
Caso 3:
La parábola no tiene raíces. En este caso, no podemos usar las raíces para encontrar la ecuación.
Obtener la ecuación
Una forma de obtener la ecuación de la parábola es hacerlo resolviendo un sistema de ecuaciones lineales a partir de 3 puntos distintos de la parábola. Sin embargo, este método puede ser engorroso, así que es preferible utilizar las propiedades vistas anteriormente: coordenadas del vértice, puntos de corte, etc.
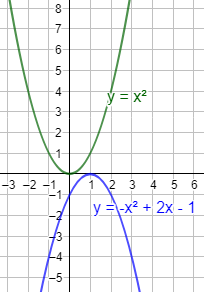
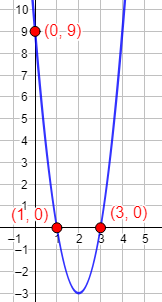
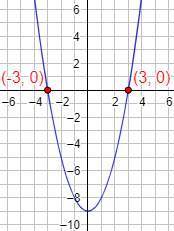
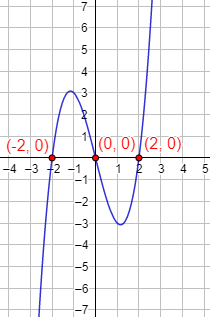
Ejemplo 1: encontrar la ecuación de la parábola que corta al eje de las abscisas en los puntos (1, 0) y (3, 0) y que pasa al eje de ordenadas en el punto (0, 9).
De los puntos de corte con el eje de abscisas sabemos que las raíces de la función parabólica son x = 1 y x = 3. Por tanto, la ecuación de la parábola es
Falta conocer el coeficiente , pero podemos hallarlo sabiendo que la parábola pasa por el punto (0, 9). Sólo tenemos que sustituir las coordenadas:
Por tanto, la ecuación de la parábola es
O bien, si calculamos los productos,
Gráfica:
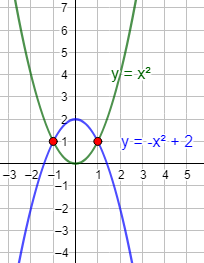
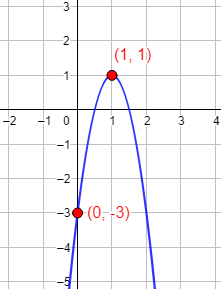
Ejemplo 2: hallar la ecuación de la parábola que tiene el vértice en el punto (1, 1) y que pasa por el punto (0, -3).
Sabemos que la primera coordenada del vértice es
Por tanto, como el vértice está en (1, 1), tenemos
Por otro lado, podemos sustituir las coordenadas del punto (0, -3) en la ecuación general de la parábola:
Sustituimos y n la ecuación:
Nos falta hallar el coeficiente , pero también podemos sustituir las coordenadas del vértice (1, 1) en la ecuación:
Luego la ecuación de la parábola es
Gráfica:
Más ejemplos y temas relacionados:

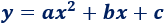
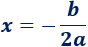
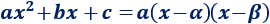
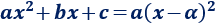
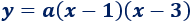
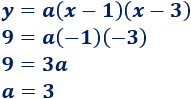
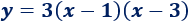

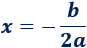
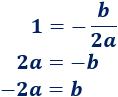
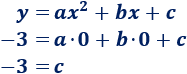
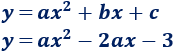
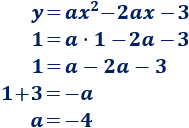
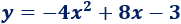
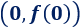
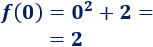
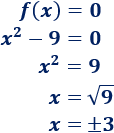
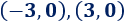

![la integral definida de f es el área de la región delimitada entre la gráfica de f, el eje OX en el intervalo [a,b] Issac Barrow (1630-1677): biografía, interpretación geométrica de la integral definida y demostración de la Regla de Barrow y del Teorema fundamental del cálculo](https://www.matesfacil.com/matematicos/Barrow/Barrow.png)