Recordad que la ecuación de la circunferencia de centro P = (a, b) y radio R es
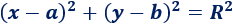
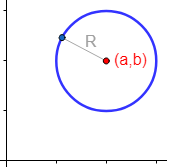
Los puntos cuyas coordenadas cumplen dicha ecuación forman parte de la circunferencia.
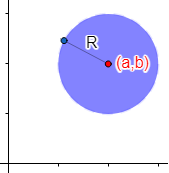
Un círculo es una circunferencia que incluye los puntos de su interior. La distancia de dichos puntos del interior hasta el centro de la circunferencia es menor que el radio. Por tanto, la ecuación del círculo de centro (a, b) y radio R es
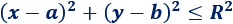
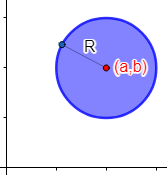
Finalmente, si no queremos el borde del círculo, escribimos el signo de desigualdad estricta:
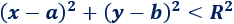
Más ejemplos y temas relacionados:
