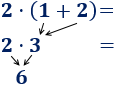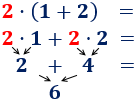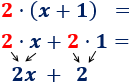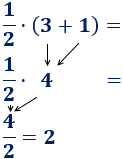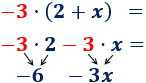Cuando un número multiplica a un paréntesis, podemos proceder de dos formas:
- Realizar las operaciones del paréntesis y multiplicar después. Por ejemplo,
- Multiplicar dicho número por todos los sumandos que contiene el paréntesis. Por ejemplo,
Ambas opciones son correctas y se obtiene el mismo resultado. No obstante, en ocasiones nos vemos obligados a la segunda opción por no poder realizar las operaciones del paréntesis. Por ejemplo,
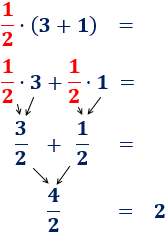
Si en lugar de una multiplicación tenemos una división, se procede del mismo modo. Por ejemplo,
O bien,
Si el número que multiplica o divide a un paréntesis en negativo, tenemos que tenerlo en cuenta al eliminar el paréntesis:
El signo negativo cambia los signos de los sumandos del paréntesis.
Ejemplo:
Más información y temas relacionados: