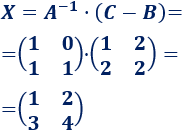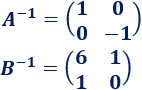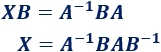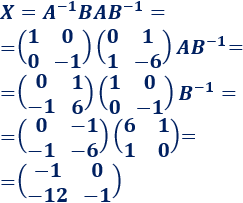Una ecuación matricial es una ecuación cuya incógnita es una matriz. Para poder resolver una ecuación matricial, tendremos que sumar, restar y multiplicar matrices y calcular matrices inversas.
Ejemplo 1 de resolución de una ecuación matricial:
donde A, B y C son las matrices siguientes:
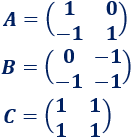
Pasamos la matriz B restando al otro lado:
La matriz A tiene inversa y es
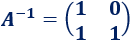
Multiplicamos la ecuación por la inversa de A para calcular la matriz solución de la ecuación:
Ejemplo 2 de resolución de una ecuación matricial:
donde A y B son las matrices siguientes:
Las matrices AA y BB tienen inversa y son
Multiplicamos la ecuación por la inversa de A:
Y por la inversa de B:
Calculamos los productos matriciales:
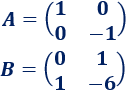
Más información y problemas de matrices:
- Suma de matrices
- Multiplicar matrices (1)
- Multiplicar matrices (2)
- Eliminación de Gauss (1)
- Eliminación de Gauss (2)
- Determinantes de matrices (1)
- Determinantes de matrices (2)
- Matriz inversa (1)
- Matriz inversa (por Gauss) (2)
- Matriz inversa (por determinantes) (3)
- Ejemplos del teorema de Rouché-Frobenius (1)
- Demostración y ejemplos del teorema de Rouché-Frobenius (2)
- Ejemplos de la regla de Cramer (1)
- Ejemplos de la regla de Cramer (2)
- Ecuaciones matriciales (1)
- Ecuaciones matriciales (2)
- Potencias enésimas de matrices (1)
- Potencias de matrices (2)
- Problemas teóricos de matrices
- Propiedades de los determinantes
- Matriz adjunta
- Más temas de matrices
Calculadoras online de matrices: