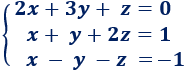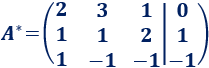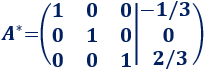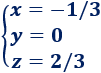Recordad que para resolver un sistema de ecuaciones podemos, sin alterar las soluciones del sistema:
- Intercambiar el orden de las ecuaciones.
- Sumar algunas de sus ecuaciones.
- Multiplicar alguna ecuación por un número distinto de 0.
Esto es precisamente lo que se hace en el método de Gauss: se modifican las ecuaciones para obtener un sistema mucho más fácil de resolver, pero, en lugar de hacerlo sobre las ecuaciones, se hace sobre la matriz ampliada del sistema.
El método de eliminación de Gauss consiste en operar sobre la matriz ampliada del sistema hasta hallar la forma escalonada (una matriz triangular superior). Así, se obtiene un sistema fácil de resolver por sustitución hacia atrás.
Si finalizamos las operaciones al hallar la forma escalonada reducida (forma lo más parecida a la matriz identidad), entonces el método se denomina eliminación de Gauss-Jordan.
- Si se obtiene la matriz identidad, el sistema es compatible determinado (como en el sistema 1).
- Si se obtiene alguna fila de ceros con término independiente distinto de 0, el sistema es incompatible (como en el sistema 2).
- Si se obtiene alguna fila de ceros y no estamos en el caso anterior, el sistema es compatible indeterminado (como en el sistema 3).
Ejemplo
La matriz ampliada del sistema es
A fila 1 le restamos dos veces la fila 3 y a la fila 2 le restamos la fila 3:
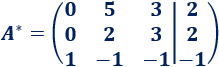
A la fila 1 le restamos la fila 2:
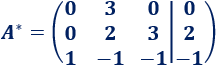
Dividimos la fila 1 entre 3:

A la fila 3 le sumamos la fila 1 y a la fila 2 le restamos dos veces la fila 1:
Dividimos la fila 2 entre 3:

A la fila 3 le sumamos la fila 2:
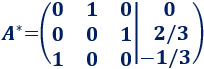
Reordenamos las 3 filas:
Ya tenemos resuelto el sistema porque la matriz obtenida es la solución:
El sistema es compatible determinado.
Más información de matrices:
- Suma de matrices
- Multiplicar matrices (1)
- Multiplicar matrices (2)
- Eliminación de Gauss (1)
- Eliminación de Gauss (2)
- Determinantes de matrices (1)
- Determinantes de matrices (2)
- Matriz inversa (1)
- Matriz inversa (por Gauss) (2)
- Matriz inversa (por determinantes) (3)
- Ejemplos del teorema de Rouché-Frobenius (1)
- Demostración y ejemplos del teorema de Rouché-Frobenius (2)
- Ejemplos de la regla de Cramer (1)
- Ejemplos de la regla de Cramer (2)
- Ecuaciones matriciales (1)
- Ecuaciones matriciales (2)
- Potencias enésimas de matrices (1)
- Potencias de matrices (2)
- Problemas teóricos de matrices
- Propiedades de los determinantes
- Matriz adjunta
- Más temas de matrices
Calculadoras online de matrices: