La matriz transpuesta (o traspuesta) de la matiz A se denota por A^T y es la matriz que tiene por filas a las columnas de A.

Si la matriz  A es de dimensión mxn, entonces la dimensión de  A^T  es nxm.

Ejemplo: suma de una matriz y de la matriz producto de un escalar por la transpuesta de una matriz:

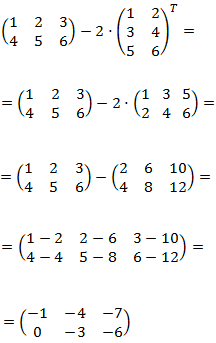
Propiedades de la transposición

• Si la matriz A es cuadrada y diagonal, A = A^T.
• La transpuesta de la transpuesta de A es A: (A^T)^T = A.
• La transpuesta de la suma de matrices es (A + B)^T = A^T + B^T.
• La transpuesta del producto de un escalar α por una matriz A es (α·A)^T = α·A^T
• La transpuesta del producto de matrices es (A·B)^T = B^T·A^T.

Recursos de matrices:

• Suma de matrices
• Multiplicar matrices (1)
• Multiplicar matrices (2)
• Eliminación de Gauss (1)
• Eliminación de Gauss (2)
• Determinantes de matrices (1)
• Determinantes de matrices (2)
• Matriz inversa (1)
• Matriz inversa (por Gauss) (2)
• Matriz inversa (por determinantes) (3)
• Ejemplos del teorema de Rouché-Frobenius (1)
• Demostración y ejemplos del teorema de Rouché-Frobenius (2)
• Ejemplos de la regla de Cramer (1)
• Ejemplos de la regla de Cramer (2)
• Ecuaciones matriciales (1)
• Ecuaciones matriciales (2)
• Potencias enésimas de matrices (1)
• Potencias de matrices (2)
• Problemas teóricos de matrices
• Propiedades de los determinantes
• Matriz adjunta
• Más temas de matrices

Calculadoras online de matrices:

• Calculadora del producto de matrices
• Calculadora de determinante de una matriz
• Calculadora de la matriz inversa
• Calculadora de la regla de Cramer