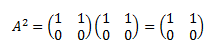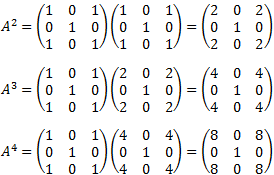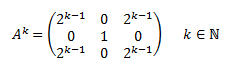Sólo podemos calcular potencias de matrices cuadradas. Por ejemplo, la potencia A2 es el producto de matrices A·A, lo que exige que A tiene que ser cuadrada.
Dedicamos una página a las potencias de matrices ya que en muchas ocasiones las potencias enésimas de una matriz tienen una determinada forma. Por ejemplo, todas las potencias de la matriz identidad son la matriz identidad: In = I para todo n natural.
Ejemplo 1: calculamos las potencias de la siguiente matriz cuadrada:
![]()
La potencia A2 es
Es inmediato que todas las potencias de A coinciden con A.
Ejemplo 2: calculamos las potencias de la siguiente matriz cuadrada:
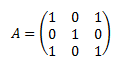
Calculamos A al cuadrado, al cubo y a la cuarta:
Existe un claro patrón:
Recursos de matrices:
-
-
- Suma de matrices
- Multiplicar matrices (1)
- Multiplicar matrices (2)
- Eliminación de Gauss (1)
- Eliminación de Gauss (2)
- Determinantes de matrices (1)
- Determinantes de matrices (2)
- Matriz inversa (1)
- Matriz inversa (por Gauss) (2)
- Matriz inversa (por determinantes) (3)
- Ejemplos del teorema de Rouché-Frobenius (1)
- Demostración y ejemplos del teorema de Rouché-Frobenius (2)
- Ejemplos de la regla de Cramer (1)
- Ejemplos de la regla de Cramer (2)
- Ecuaciones matriciales (1)
- Ecuaciones matriciales (2)
- Potencias enésimas de matrices (1)
- Potencias de matrices (2)
- Problemas teóricos de matrices
- Propiedades de los determinantes
- Matriz adjunta
- Más temas de matrices
-
Calculadoras online de matrices: