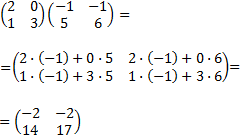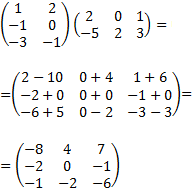El producto de matrices es quizás la operación más complicada de realizar, al menos, las primeras veces. Vamos primero a explicarlo de forma sencilla.
Supongamos que las matrices A y B son de dimensión 2×2. El resultado del producto de la matriz A y de la matriz B es la matriz de dimensión 2×2 que denotamos por AB y sus elementos son:
- El elemento de la posición (1,1) de la matriz AB es el producto de la fila 1 de A y de la columna 1 de B.
- El elemento de la posición (1,2) de la matriz AB es el producto de la fila 1 de A y de la columna 2 de B.
- El elemento de la posición (2,1) de la matriz AB es el producto de la fila 2 de A y de la columna 1 de B.
- El elemento de la posición (2,2) de la matriz AB es el producto de la fila 2 de A y de la columna 2 de B.
Hemos dicho producto de una fila por una matriz. Este producto no es más que el producto escalar de dos vectores: vector fila por vector columna. Por ejemplo, el producto de la fila (1,2,3) y (4,5,6) es 1·4 + 2·5 + 3·6 = 32.
Ejemplo: producto de dos matrices de dimensión 2×2:
Para poder multiplicar los vectores fila y columna, éstos tienen que ser de la misma dimensión. Esto implica que el número de columnas de la matriz A debe coincidir con el número de filas de la matriz B.
Es decir, para calcular el producto A·B la dimensión de A debe ser mxn y la de B debe ser nxk. La matriz producto A·B es de dimensión mxk.
Ejemplo: producto de dos matrices con dimensiones distintas:
Algunas propiedades
La propiedad más destacable del producto de matrices es que no es conmutativo. Es decir, el producto A·B no tiene porqué coincidir con el producto B·A. De hecho, si las matrices no son cuadradas, uno de los dos productos no se puede calcular.
Otras propiedades:
- Es asociativo
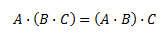
- Es distributivo (por la derecha) respecto de la suma
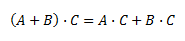
- Es distributivo (por la izquierda) respecto de la suma
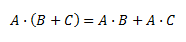
- El producto de matrices tiene elemento neutro y es la matriz identidad con la dimensión adecuada para poder calcular el producto. Es decir, si la matriz A es de dimensión mxn, entonces
A·In = A = Im·A
Recursos de matrices:
- Suma de matrices
- Multiplicar matrices (1)
- Multiplicar matrices (2)
- Eliminación de Gauss (1)
- Eliminación de Gauss (2)
- Determinantes de matrices (1)
- Determinantes de matrices (2)
- Matriz inversa (1)
- Matriz inversa (por Gauss) (2)
- Matriz inversa (por determinantes) (3)
- Ejemplos del teorema de Rouché-Frobenius (1)
- Demostración y ejemplos del teorema de Rouché-Frobenius (2)
- Ejemplos de la regla de Cramer (1)
- Ejemplos de la regla de Cramer (2)
- Ecuaciones matriciales (1)
- Ecuaciones matriciales (2)
- Potencias enésimas de matrices (1)
- Potencias de matrices (2)
- Problemas teóricos de matrices
- Propiedades de los determinantes
- Matriz adjunta
- Más temas de matrices
Calculadoras online de matrices: