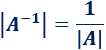Propiedades de los determinantes

• Se puede extraer factor común de una fila o columna multiplicando el determinante por el factor.
• Se puede extraer el mismo factor común de n filas o columnas multiplicando el determinante por el factor elevado a n.
• Si se cambia el orden de una fila o de una columna, el determinante cambia de signo.
• Si se cambia el orden de n filas o columnas, el determinante cambia de signo si n es impar.
• Si una matriz es invertible, el determinante de la inversa es el inverso del determinante:

• El determinante de una matriz es igual al de su traspuesta:

• Si una matriz tiene filas o columnas linealmente dependientes, entonces su determinante es 0.
• El determinante no cambia si se suman filas (o columnas) multiplicadas por números distintos de 0.
• El determinante de una matriz diagonal es el producto de los elementos de su diagonal.

Más información y problemas resueltos de matrices:

• Suma de matrices
• Multiplicar matrices (1)
• Multiplicar matrices (2)
• Eliminación de Gauss (1)
• Eliminación de Gauss (2)
• Determinantes de matrices (1)
• Determinantes de matrices (2)
• Matriz inversa (1)
• Matriz inversa (por Gauss) (2)
• Matriz inversa (por determinantes) (3)
• Ejemplos del teorema de Rouché-Frobenius (1)
• Demostración y ejemplos del teorema de Rouché-Frobenius (2)
• Ejemplos de la regla de Cramer (1)
• Ejemplos de la regla de Cramer (2)
• Ecuaciones matriciales (1)
• Ecuaciones matriciales (2)
• Potencias enésimas de matrices (1)
• Potencias de matrices (2)
• Problemas teóricos de matrices
• Propiedades de los determinantes
• Matriz adjunta
• Más temas de matrices

Calculadoras online de matrices:

• Calculadora del producto de matrices
• Calculadora de determinante de una matriz
• Calculadora de la matriz inversa
• Calculadora de la regla de Cramer