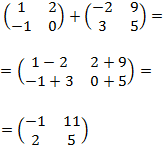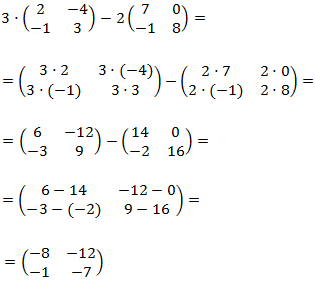Suma de matrices
La suma de dos matrices de igual dimensión tiene como resultado una matriz de la misma dimensión.
La matriz suma de dos matrices con la misma dimensión es la matriz que tiene en la posición fila i y columna j la suma de los elementos de dicha posición en las matrices que sumamos.
Ejemplo: suma de dos matrices cuadradas de dimensión 2:
La resta se calcula de forma análoga.
Observaciones:
- Para sumar/restar dos matrices, tienen que tener la misma dimensión.
- La suma de matrices es conmutativa: A+B = B+A.
Producto de un escalar por una matriz
El resultado del producto de un escalar (un número real) por una matriz es una matriz con la misma dimensión. Dicha matriz se calcula multiplicando todas sus entradas por el escalar.
Ejemplo: en la siguiente operación tenemos dos productos de escalar por una matriz y un resta de matrices:
Observaciones:
- El producto de una matriz A por un escalar α es conmutativo: A·α = α·A.
- La dimensión de la matriz α·A es la misma que la de A.
Recursos de matrices:
- Suma de matrices
- Multiplicar matrices (1)
- Multiplicar matrices (2)
- Eliminación de Gauss (1)
- Eliminación de Gauss (2)
- Determinantes de matrices (1)
- Determinantes de matrices (2)
- Matriz inversa (1)
- Matriz inversa (por Gauss) (2)
- Matriz inversa (por determinantes) (3)
- Ejemplos del teorema de Rouché-Frobenius (1)
- Demostración y ejemplos del teorema de Rouché-Frobenius (2)
- Ejemplos de la regla de Cramer (1)
- Ejemplos de la regla de Cramer (2)
- Ecuaciones matriciales (1)
- Ecuaciones matriciales (2)
- Potencias enésimas de matrices (1)
- Potencias de matrices (2)
- Problemas teóricos de matrices
- Propiedades de los determinantes
- Matriz adjunta
- Más temas de matrices
Calculadoras online de matrices: