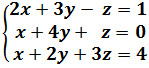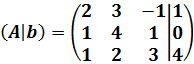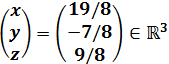El teorema de Rouché-Frobenius es de gran importancia en el Álgebra. En esta página vamos a enunciar el teorema y a ver un ejemplo de aplicación.
Teorema de Rocuhé-Frobenius
Sea el sistema de ecuaciones en forma matricial Ax = b, donde A es la matriz de coeficientes, b es la matriz columna de términos independientes y x la matriz columna de incógnitas. Consideramos que el sistema tiene m ecuaciones y n incógnitas, así que la dimensión de A es mxn y la dimensión de x y de b es nx1.
El teorema establece que
- El sistema Ax = b es compatible si el rango de la matriz A coincide con el rango de la matriz ampliada (A|b).
- El sistema Ax = b es compatible determinado si el rango de la matriz A y el de la matriz ampliada (A|b) es igual a n.
Ejemplo de aplicación
Consideremos el sistema de ecuaciones
La matriz ampliada del sistema es:
El rango de la matriz es
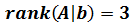
ya que tiene un determinante de dimensión 3 no nulo:
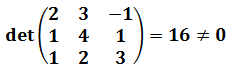
Además, como el determinante anterior también es el determinante de la matriz A, la matriz de coeficientes también tiene rango 3:
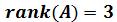
Por tanto, tenemos que los rangos de las dos matrices coinciden
y, por el teorema de Rouché-Frobenius, como el rango es igual al número de incógnitas, el sistema es compatible determinado.
En efecto, la única solución del sistema es, en forma matricial,
Recursos de matrices:
- Suma de matrices
- Multiplicar matrices (1)
- Multiplicar matrices (2)
- Eliminación de Gauss (1)
- Eliminación de Gauss (2)
- Determinantes de matrices (1)
- Determinantes de matrices (2)
- Matriz inversa (1)
- Matriz inversa (por Gauss) (2)
- Matriz inversa (por determinantes) (3)
- Ejemplos del teorema de Rouché-Frobenius (1)
- Demostración y ejemplos del teorema de Rouché-Frobenius (2)
- Ejemplos de la regla de Cramer (1)
- Ejemplos de la regla de Cramer (2)
- Ecuaciones matriciales (1)
- Ecuaciones matriciales (2)
- Potencias enésimas de matrices (1)
- Potencias de matrices (2)
- Problemas teóricos de matrices
- Propiedades de los determinantes
- Matriz adjunta
- Más temas de matrices
Calculadoras online de matrices: