Función derivable y derivada
Sean I un intervalo abierto de los reales, a un punto de I y f una función de I en los reales. Entonces, decimos que f es derivable en a si existe el siguiente límite y, en tal caso, a su valor le llamaremos f ‘(a):
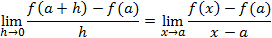
Decimos que f es derivable en I si lo es en todos los puntos del intervalo. Llamamos derivada de f a la función f ‘(x) siendo x de I.
Derivadas elementales
Llamamos derivadas elementales o inmediatas a aquéllas que luego utilizaremos para el cálculo de derivadas de funciones más complejas. Por ejemplo, derivada de una potencia, de una constante, del seno, de la exponencial, etc.
Recogemos las derivadas elementales en la siguiente tabla: tabla de derivadas y reglas de derivación.
Reglas de derivación
- Derivada del producto por una constante: Sean f derivable en a y k una constante, entonces
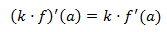
- Derivada del producto: Sean f y g dos funciones derivables en a, entonces,
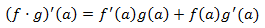
- Derivada del cociente: Sean f y g funciones derivables en a siendo g ( a ) ≠ 0, entonces
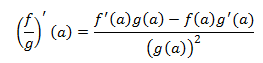
- Derivada de la inversa: Sea f derivable en el punto a tal que la derivada en dicho punto no se anula, esto es, f ‘ (a) no es 0, y existe la inversa de f en un entorno de f (a), entonces
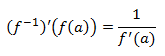
Recursos de cálculo diferencial:
- Concepto de derivada
- Tabla de derivadas (pdf)
- Problemas de calcular derivadas
- Problemas de extremos relativos (máximos y mínimos)
- Criterio de la primera derivada
- Criterio de la segunda derivada
- Condición necesaria de extremos relativos
- Problemas de monotonía y curvatura de funciones
- Límites resueltos por L’Hôpital
- Problemas de optimizar (cálculo diferencial)
