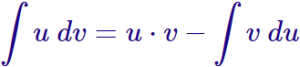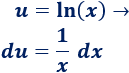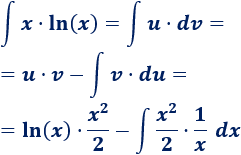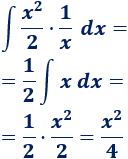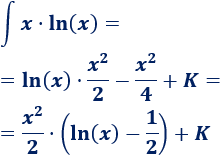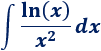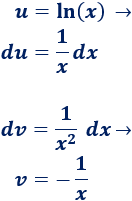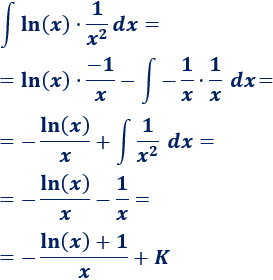En esta página proporcionamos dos ejemplos del método de integración por partes.
Este método consiste en la aplicación de la siguiente fórmula:
Tenemos que identificar los términos u y dv en la integral, después,
- calculamos du derivando u
- calculamos v integrando dv
Ejemplo 1
El integrando es un producto de dos funciones.
1. Escogemos u y dv
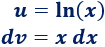2. Calculamos du y v
Para calcular du tenemos que derivar u:
Para calcular v tenemos que integrar dv:
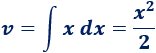3. Aplicamos la fórmula
Sólo tenemos que sustituir las variables de la fórmula:
4. Calculamos la integral que queda
La integral que queda es inmediata:
Por tanto,
Nota: la elección de u y dv a veces no es fácil. Por ejemplo, en esta integral, si escogemos dv = ln(x)dx, no podemos calcular v.
Ejemplo 2
Es más intuitivo si escribimos el radicando como un producto:
1. Escogemos u y dv y calculamos du y v
2. Aplicamos la fórmula
Más integrales resueltas: