Supongamos que la función F(x) es una primitiva de f(x), es decir, que la derivada de F(x) es f(x):
F'(x) = f(x)
O bien, la función F(x) es la integral de f(x):
La integral definida de la función f(x) en el intervalo [a, b] es
La regla de Barrow es un teorema que proporciona la integral definida de f(x) en términos de una primitiva de f(x):
Veamos algunos ejemplos:
Ejemplo 1
Calculamos la integral definida de f(x) = x2 en el intervalo [0, 2]:
Una primitiva de x2 es x3/3, así que, por la regla de Barrow,
Ejemplo 2
Calculamos la integral definida de f(x) = x2 -4x +3 en el intervalo [0, 1]:
Y en el intervalo [1, 2]:
Más ejemplos y temas relacionados:
- Integral definida (teoría)
- Integrales definidas (áreas), 1
- Integrales definidas (áreas), 2
- Integrales directas
- Integración por partes
- Integración por sustitución
- Integrales de funciones racionales

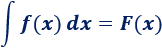
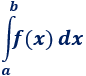
![Regla de Barrow: la integral definida de f(x) en [a,b] es F(b)-F(a) Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/T1.png)
![calculamos la integral definida de x^2 en el intervalo [0,2], obteniendo 8/3 Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/T3.png)
![calculamos la integral definida de x^2-4x+3 en [0,1], obteniendo 4/3 Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/T9.png)
![calculamos la integral definida de x^2-4x+3 en [1,2], obteniendo -2/3 Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/T10.png)