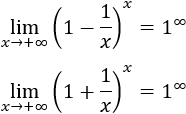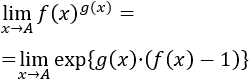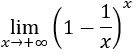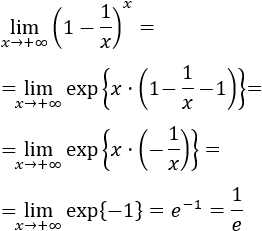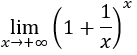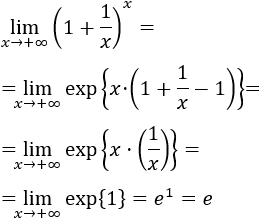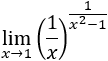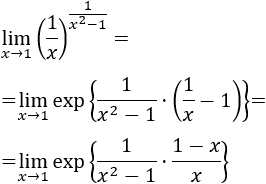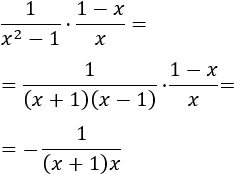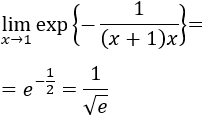En esta página proporcionamos la fórmula que permite resolver la indeterminación uno elevado a infinito y tres ejemplos de aplicación de la misma.
1. Indeterminación 1∞
Uno elevado a infinito es una forma indeterminada puesto que aparece en el cálculo de límites de funciones cuyos límites son distintos.
Por ejemplo, aparece en los siguientes límites:
Sin embargo, el primer límite es igual a 1/e y el segundo es igual a e.
2. Fórmula
La indeterminación 1∞ es una de las más sencillas de resolver puesto que disponemos de una sencilla fórmula:
siendo f(x) y g(x) funciones que tienden a 1 y a ∞, respectivamente, cuando x tiende al punto A (A puede ser infinito).
Por comodidad a la hora de escribir las expresiones matemáticas, escribiremos la exponencial en la forma exp{·}, es decir,
Asumiendo esta notación, la fórmula anterior vista para la indeterminación es
3. Ejemplos de aplicación
Ejemplo 1
Solución:
Aplicamos la fórmula:
Ejemplo 2
Solución:
Aplicamos la fórmula:
Ejemplo 3
Solución:
Aplicamos la fórmula:
Podemos simplificar el exponente:
Calculamos el límite:
Más ejemplos en indeterminación 1 elevado a infinito.
Temas de límites:
- 50 límites resueltos
- Límites resueltos
- Límites laterales
- Indeterminación (límites de funciones)
- Indeterminación infinito menos infinito
- Indeterminación cero partido cero
- Indeterminación infinito partido infinito
- Indeterminación cero por infinito
- Indeterminación uno elevado a infinito
- Indeterminación cero elevado cero
- Indeterminación infinito elevado a cero
- Regla de L’Hôpital
- Infinitésimos equivalentes
- Teorema del emparedado
- Límites de sucesiones
- Definiciones formales de límites
- Criterio de la media geométrica y de la raíz
- Criterio de la media aritmética
- Criterio de Stolz del cociente