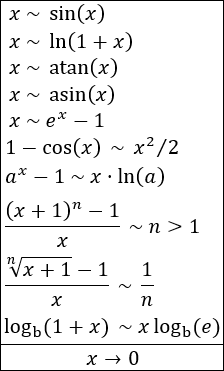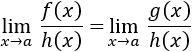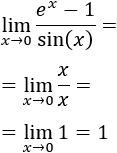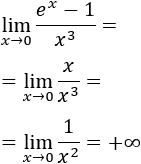En esta página explicamos qué son los infinitésimos equivalentes y mostramos dos ejemplos de su aplicación en el cálculo de límites.

1. Conceptos

Decimos que f(x) es un infinitésimo en x=a si su límite en dicho punto es 0, es decir, si

Decimos que f(x) y g(x) son infinitésimos equivalentes en x=a si son infinitésimos en x=a y, además,

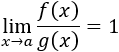
Lo expresamos mediante

2. Ejemplos

Algunos infinitésimos equivalentes en x=0 son los siguientes:

3. Cálculo de límites

La aplicación de infinitésimos equivalentes en el cálculo de límites se basa el siguiente resultado:

Si dos funciones f(x) y g(x) son infinitésimos equivalentes en x=a, podemos intercambiar f(x) por g(x) en los límites cuando x tiende a a en los que f(x) multiplica o divide a otra función.
Es decir,

Y también,

4. Ejemplos

Ejemplo 1

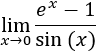
Solución:

Teniendo en cuenta la tabla vista, tanto el numerador y como el denominador son infinitésimos equivalentes a la función f(x)=x. Por tanto,

Ejemplo 2

Solución:

Como el numerador es un infinitésimo equivalente a la función f(x)=x,

 

Más ejemplos en infinitésimos equivalentes.

 

Temas de límites:

• 50 límites resueltos
• Límites resueltos
• Límites laterales
• Indeterminación (límites de funciones)
• Indeterminación infinito menos infinito
• Indeterminación cero partido cero
• Indeterminación infinito partido infinito
• Indeterminación cero por infinito
• Indeterminación uno elevado a infinito
• Indeterminación cero elevado cero
• Indeterminación infinito elevado a cero
• Regla de L’Hôpital
• Infinitésimos equivalentes
• Teorema del emparedado
• Límites de sucesiones
• Definiciones formales de límites
• Criterio de la media geométrica y de la raíz
• Criterio de la media aritmética
• Criterio de Stolz del cociente