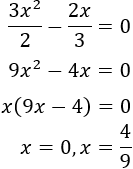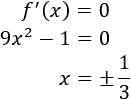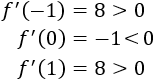Criterio de la primera derivada

Sea f una función continua en el intervalo [a, b] y derivable en ]a, b[. Entonces,

  • La función f es monótona creciente en el intervalo ]a, b[ si, y sólo si, f'(x)≥0 para todo x∈]a, b[.
  • La función f es monótona decreciente en el intervalo ]a, b[ si, y sólo si, f'(x)≤0 para todo x∈]a, b[.

Decimos que c∈]a, b[ es un punto crítico si f'(x)=0.

 

Los puntos críticos son los candidatos a ser extremos relativos (y absolutos) de la función.

Aplicaciones

Además de la proporcionar la monotonía de la función, el criterio de la primera derivada se utiliza para hallar extremos relativos y determinar su tipo (máximo o mínimo).

Si c es un punto crítico de f, entonces:

  • Si f es creciente a la izquierda de c y decreciente a su derecha, c es un máximo.
  • Si f es decreciente a la izquierda de c y creciente a su derecha, c es un mínimo.
  • Si la monotonía de f es igual a ambos lados de c, entonces c no es un extremo relativo.

Ejemplo 1

Demostrar que la siguiente función es monótona creciente para x>4/9:

Enunciamos y demostramos la regla o criterio de la primera derivada y proporcionamos algunos ejemplos. El criterio proporciona la monotonía de la función y deducir la existencia de extremos relativos (máximos y mínimos). Matemáticas. Análisis y cálculo diferencial.

Derivamos la función:

Enunciamos y demostramos la regla o criterio de la primera derivada y proporcionamos algunos ejemplos. El criterio proporciona la monotonía de la función y deducir la existencia de extremos relativos (máximos y mínimos). Matemáticas. Análisis y cálculo diferencial.

Calculamos los puntos críticos:

Enunciamos y demostramos la regla o criterio de la primera derivada y proporcionamos algunos ejemplos. El criterio proporciona la monotonía de la función y deducir la existencia de extremos relativos (máximos y mínimos). Matemáticas. Análisis y cálculo diferencial.

El signo de la derivada se mantiene constante en el intervalo x>4/9. Determinamos su signo calculando la imagen de cualquier punto de dicho intervalo:

Enunciamos y demostramos la regla o criterio de la primera derivada y proporcionamos algunos ejemplos. El criterio proporciona la monotonía de la función y deducir la existencia de extremos relativos (máximos y mínimos). Matemáticas. Análisis y cálculo diferencial.

Por tanto, la función f es monótona creciente en el intervalo (4/9, +∞).

Gráfica:

Enunciamos y demostramos la regla o criterio de la primera derivada y proporcionamos algunos ejemplos. El criterio proporciona la monotonía de la función y deducir la existencia de extremos relativos (máximos y mínimos). Matemáticas. Análisis y cálculo diferencial.

Nota: no hemos estudiado la monotonía en el resto de los reales.

Ejemplo 2

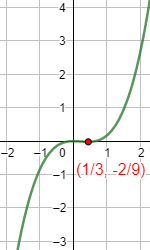
Hallar los extremos de la siguiente función polinómica:

Enunciamos y demostramos la regla o criterio de la primera derivada y proporcionamos algunos ejemplos. El criterio proporciona la monotonía de la función y deducir la existencia de extremos relativos (máximos y mínimos). Matemáticas. Análisis y cálculo diferencial.

Calculamos su derivada:

Enunciamos y demostramos la regla o criterio de la primera derivada y proporcionamos algunos ejemplos. El criterio proporciona la monotonía de la función y deducir la existencia de extremos relativos (máximos y mínimos). Matemáticas. Análisis y cálculo diferencial.

Calculamos los puntos críticos:

Enunciamos y demostramos la regla o criterio de la primera derivada y proporcionamos algunos ejemplos. El criterio proporciona la monotonía de la función y deducir la existencia de extremos relativos (máximos y mínimos). Matemáticas. Análisis y cálculo diferencial.

Hay dos puntos críticos: x=1/3 y x=-1/3.

Obviamente, el signo de la derivada se mantiene constante en los intervalos (-∞, -1/3), (-1/3, 1/3) y  (1/3, +∞), así que podemos evaluar la derivada en cualquier punto de cada intervalo para determinar su signo:

Enunciamos y demostramos la regla o criterio de la primera derivada y proporcionamos algunos ejemplos. El criterio proporciona la monotonía de la función y deducir la existencia de extremos relativos (máximos y mínimos). Matemáticas. Análisis y cálculo diferencial.

Por tanto,

  • La función f es creciente en (-∞, -1/3).
  • La función f es decreciente en (-1/3, 1/3).
  • La función f es creciente en (1/3, +∞).

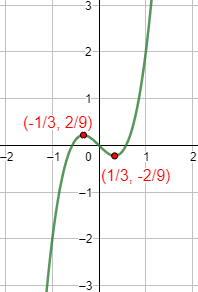
Por tanto, deducimos que x=-1/3 es un máximo y x=1/3 es un mínimo.

Teniendo en cuenta que los límites de f cuando x→±∞ son infinitos, los extremos no son absolutos.

Gráfica:

Enunciamos y demostramos la regla o criterio de la primera derivada y proporcionamos algunos ejemplos. El criterio proporciona la monotonía de la función y deducir la existencia de extremos relativos (máximos y mínimos). Matemáticas. Análisis y cálculo diferencial.

Enlaces con problemas de funciones: