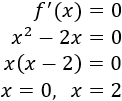Sea f una función dos veces derivable en el intervalo ]a, b[ y sea z∈]a, b[ tal que f'(z)=0. Entonces,

• Si f”(z)<0, entonces f tiene un máximo relativo en z.
• Si f”(z)>0, entonces f tiene un mínimo relativo en z.

Aplicación

La aplicación directa del criterio de la segunda derivada es determinar si los puntos críticos de una función (puntos que anulan la primera derivada) son máximos o mínimos.

Si hay extremos, podemos deducir la monotonía de la función alrededor de éstos.

Además de esto, los puntos que anulan la segunda derivada son candidatos a ser puntos de inflexión (puntos donde la curvatura de la función cambia de tipo (concavidad y convexidad)).

Ejemplo

Determinar si los extremos de la siguiente función son máximos o mínimos:

Calculamos la primera derivada:

Calculamos los puntos críticos:

Calculamos la segunda derivada:

Evaluamos la segunda derivada en los puntos críticos:

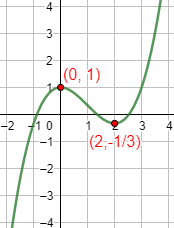
Por tanto, f tiene un máximo local en x=0 y un mínimo local en x=2.

Gráfica:

Enlaces con problemas de funciones:

• • Dominio y recorrido (1)
  • Dominio y recorrido (2)
  • Funciones lineales
  • Funciones cuadráticas
  • Rectas y parábolas
  • Funciones polinómicas
  • Funciones definidas a trozos (1)
  • Funciones definidas a trozos (2)
  • Problemas de funciones (1)
  • Problemas de funciones (2)
  • Funciones continuas (1)

• Funciones continuas (2)
• Función inversa (1)
• Función inversa (2)
• Función inyectiva, sobreyectiva y biyectiva
• Asíntotas (1)
• Asíntotas (2)
• Máximos y mínimos (1)
• Máximos y mínimos (2)
• Criterio de la primera derivada
• Criterio de la segunda derivada
• Problemas de optimizar (1)
• Problemas de optimizar (2)
• Límites (1)
• Límites (2)
• Función par y función impar
• Cálculo de derivadas
• Teorema del emparedado