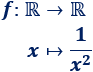Recordad que una función matemática, f, relaciona cada número a de un conjunto A con un único número b = f(a) (llamado imagen de a) de otro conjunto B. Esto se expresa mediante f:A→B.
Ejemplo
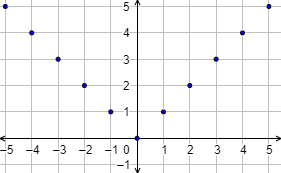
La siguiente función relaciona cada número entero con su valor absoluto:
Por ejemplo,
- La imagen de -1 es 1:
- La imagen de 1 es 1:
- La imagen de -2 es 2:
- La imagen de -5 es 5:
- La imagen de 0 es 0:
Gráfica:
La función f está definida sobre los números enteros. Este conjunto es el dominio de la función.
El conjunto de las imágenes del dominio es el conjunto de los números naturales. Este conjunto es la imagen, el recorrido o el rango de la función.
Nota: la función valor absoluto también puede definirse sobre todos los reales, los enteros, los racionales o cualquier subconjunto los números complejos.
El dominio de una función es el conjunto sobre el que se define la función (es el conjunto A).
La imagen, recorrido o rango de una función es el conjunto de las imágenes de los elementos de su dominio (es el conjunto B).
Muchas veces, por simplificar, se proporcionan un dominio y un recorrido genéricos. En este caso, se llama codominio al recorrido genérico y este conjunto contiene como subconjunto al recorrido de la función. Veamos un ejemplo:
Ejemplo
Sea la función racional
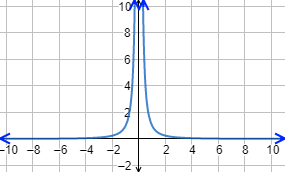
Gráfica:
Esta función se ha definido sobre los números reales pero, en realidad, la función no está definida en todos los reales. Más exactamente, la función no está definida en 0 porque no se puede calcular su imagen: f(0) = 1/0
El dominio de esta función es todos los reales excepto 0:
Además de esto, ninguna imagen es negativa ni 0 (puesto que el inverso del cuadrado de un número no nulo es siempre positivo). La imagen de la función son los números reales positivos:
Casos generales
Cada función tiene un dominio y un recorrido distintos, pero tenemos algunas reglas generales:
- El dominio y la imagen de una función polinómica es el conjunto de los reales.
- El dominio de un logaritmo es el conjunto de los reales que hacen su argumento positivo.
- El dominio de una función racional es el conjunto de los reales excepto los números que anulan el denominador.
- El dominio de una raíz de orden par es el conjunto de los reales que hacen su radicando no negativo. El recorrido es un subconjunto de los reales no negativos.
Ejemplo
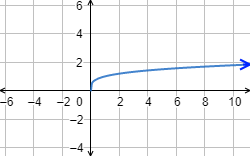
Sea la función raíz cuarta:
Como el orden de la raíz es par, su dominio y su imagen es
Gráfica:
Enlaces con problemas:
- Dominio y recorrido (1)
- Dominio y recorrido (2)
- Funciones lineales
- Funciones cuadráticas
- Rectas y parábolas
- Funciones polinómicas
- Funciones definidas a trozos (1)
- Funciones definidas a trozos (2)
- Problemas de funciones (1)
- Problemas de funciones (2)
- Funciones continuas (1)
- Funciones continuas (2)
- Función inversa (1)
- Función inversa (2)
- Función inyectiva, sobreyectiva y biyectiva
- Asíntotas (1)
- Asíntotas (2)
- Máximos y mínimos (1)
- Máximos y mínimos (2)
- Criterio de la primera derivada
- Criterio de la segunda derivada
- Problemas de optimizar (1)
- Problemas de optimizar (2)
- Límites (1)
- Límites (2)
- Función par y función impar
- Cálculo de derivadas
- Teorema del emparedado