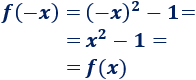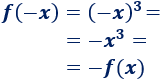Función par
Una función f es par si
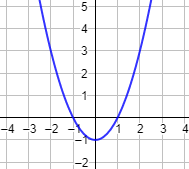
Las gráficas de las funciones pares presentan simetría respecto al eje de ordenadas.
Ejemplo:
La siguiente función es par:
Demostración:
Gráfica:
Función impar
Una función f es impar si
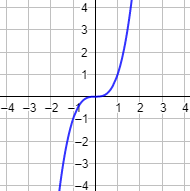
Las gráficas de las funciones impares presentan simetría rotacional con respecto al origen. Es decir, la gráfica no cambia si se rota 180°.
Ejemplo:
La siguiente función es par:
Demostración:
Gráfica:
Podéis encontrar algunas propiedades de las funciones pares e impares en paridad de funciones.
Enlaces con problemas de funciones:
- Dominio y recorrido (1)
- Dominio y recorrido (2)
- Funciones lineales
- Funciones cuadráticas
- Rectas y parábolas
- Funciones polinómicas
- Funciones definidas a trozos (1)
- Funciones definidas a trozos (2)
- Problemas de funciones (1)
- Problemas de funciones (2)
- Funciones continuas (1)
- Funciones continuas (2)
- Función inversa (1)
- Función inversa (2)
- Función inyectiva, sobreyectiva y biyectiva
- Asíntotas (1)
- Asíntotas (2)
- Máximos y mínimos (1)
- Máximos y mínimos (2)
- Criterio de la primera derivada
- Criterio de la segunda derivada
- Problemas de optimizar (1)
- Problemas de optimizar (2)
- Límites (1)
- Límites (2)
- Función par y función impar
- Cálculo de derivadas
- Teorema del emparedado