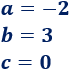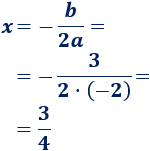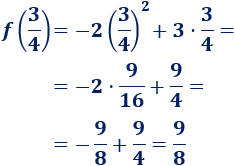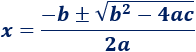Una función cuadrática (o parabólica) es una función polinómica de segundo grado. Es decir, tiene la forma
siendo a≠0.
Esta forma de escribir la función se denomina forma general.
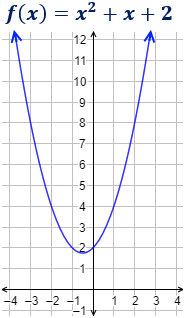
Ejemplo
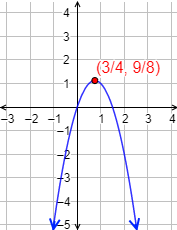
La gráfica de una función cuadrática siempre es una parábola.
Las parábolas tienen forma de (si a>0) o de (si a<0).
Además de la orientación, el coeficiente a es la causa de la amplitud de la función: cuanto mayor es |a|, más rápido crece (o decrece) la parábola, por lo que es más cerrada.
Vértice
Las funciones cuadráticas tienen un máximo (si a<0) o un mínimo (si a>0). Este punto es el vértice de la parábola.
La primera coordenada del vértice es
Y la segunda coordenada es su imagen:
Ejemplo
Calculamos el vértice de la función
Identificamos los coeficientes:
Como a es negativo, la parábola tiene forma de . El vértice es un máximo.
La primera coordenada del vértice es
Calculamos la segunda coordenada:
Por tanto, el vértice es el punto
Gráfica:
Puntos de corte
Una parábola siempre corta el eje de ordenadas (eje Y) en un punto. Como esto ocurre cuando x=0, se trata del punto (0,c) puesto que f(0)=c.
Una función corta al eje de abscisas cuando y=0. Por tanto, para hallar estos puntos de corte, tenemos que resolver una ecuación cuadrática:
Como una ecuación cuadrática puede tener una, dos o ninguna solución, puede haber uno, dos o ningún punto de corte con el eje X.
Recordamos la fórmula que necesitamos:
Forma canónica
La forma canónica de una función cuadrática es
donde a es el coeficiente principal visto ya; h es la primera coordenada del vértice y k es la segunda.
Enlaces con problemas:
- Dominio y recorrido (1)
- Dominio y recorrido (2)
- Funciones lineales
- Funciones cuadráticas
- Rectas y parábolas
- Funciones polinómicas
- Funciones definidas a trozos (1)
- Funciones definidas a trozos (2)
- Problemas de funciones (1)
- Problemas de funciones (2)
- Funciones continuas (1)
- Funciones continuas (2)
- Función inversa (1)
- Función inversa (2)
- Función inyectiva, sobreyectiva y biyectiva
- Asíntotas (1)
- Asíntotas (2)
- Máximos y mínimos (1)
- Máximos y mínimos (2)
- Criterio de la primera derivada
- Criterio de la segunda derivada
- Problemas de optimizar (1)
- Problemas de optimizar (2)
- Límites (1)
- Límites (2)
- Función par y función impar
- Cálculo de derivadas
- Teorema del emparedado