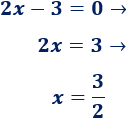Funciones lineales

Una función lineal es una función polinómica de primer grado. Es decir, tiene la siguiente forma

Definimos función lineal y explicamos algunos conceptos: pendiente, ordenada, gráfica, punto de corte con los ejes, intersección de dos funciones, rectas paralelas y perpendiculares. Finalmente, resolvemos problemas de aplicación. Matemáticas. Secundaria.

siendo m≠0.

  • m es la pendiente de la función
  • n es la ordenada (en el origen) de la función

La gráfica de una función lineal es siempre una recta.

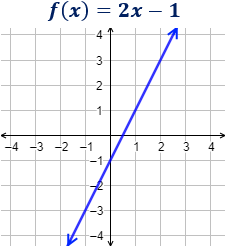
Ejemplo:

Definimos función lineal y explicamos algunos conceptos: pendiente, ordenada, gráfica, punto de corte con los ejes, intersección de dos funciones, rectas paralelas y perpendiculares. Finalmente, resolvemos problemas de aplicación. Matemáticas. Secundaria.

La pendiente de la recta es m = 2 y la ordenada es n = -1.

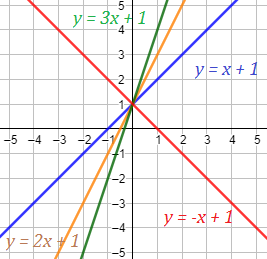
Geométricamente, cuanto mayor es la pendiente, más inclinada es la recta. Es decir, más rápido crece la función.

  • Si la pendiente es positiva, la función es creciente.
  • Si la pendiente es negativa, la función es decreciente.

Ejemplo:

Rectas con pendientes 1, 2, 3 y -1:

Definimos función lineal y explicamos algunos conceptos: pendiente, ordenada, gráfica, punto de corte con los ejes, intersección de dos funciones, rectas paralelas y perpendiculares. Finalmente, resolvemos problemas de aplicación. Matemáticas. Secundaria.

Puntos de corte

Una función lineal siempre corta al eje Y en un punto. También, corta al eje X en un punto.

El punto de corte con el eje Y es el punto de la recta que tiene la primera coordenada igual a 0:

Definimos función lineal y explicamos algunos conceptos: pendiente, ordenada, gráfica, punto de corte con los ejes, intersección de dos funciones, rectas paralelas y perpendiculares. Finalmente, resolvemos problemas de aplicación. Matemáticas. Secundaria.

El punto de corte con el eje X es el punto de la recta que tiene 0 en la segunda coordenada. Se calcula igualando a 0 la función y resolviendo la ecuación obtenida.

Ejemplo:

Calculamos los puntos de corte de la función del ejemplo anterior,

Definimos función lineal y explicamos algunos conceptos: pendiente, ordenada, gráfica, punto de corte con los ejes, intersección de dos funciones, rectas paralelas y perpendiculares. Finalmente, resolvemos problemas de aplicación. Matemáticas. Secundaria.

Corte con el eje Y:

Definimos función lineal y explicamos algunos conceptos: pendiente, ordenada, gráfica, punto de corte con los ejes, intersección de dos funciones, rectas paralelas y perpendiculares. Finalmente, resolvemos problemas de aplicación. Matemáticas. Secundaria.

Es el punto

Definimos función lineal y explicamos algunos conceptos: pendiente, ordenada, gráfica, punto de corte con los ejes, intersección de dos funciones, rectas paralelas y perpendiculares. Finalmente, resolvemos problemas de aplicación. Matemáticas. Secundaria.

Observad que la segunda coordenada es la ordenada.

Corte con el eje X:

Definimos función lineal y explicamos algunos conceptos: pendiente, ordenada, gráfica, punto de corte con los ejes, intersección de dos funciones, rectas paralelas y perpendiculares. Finalmente, resolvemos problemas de aplicación. Matemáticas. Secundaria.

Es el punto

Definimos función lineal y explicamos algunos conceptos: pendiente, ordenada, gráfica, punto de corte con los ejes, intersección de dos funciones, rectas paralelas y perpendiculares. Finalmente, resolvemos problemas de aplicación. Matemáticas. Secundaria.

Función a partir de dos puntos

Si tenemos dos puntos de la recta, podemos calcular la expresión algebraica de la función. Sólo tenemos que sustituir las coordenadas de los puntos en la forma general de la función

Definimos función lineal y explicamos algunos conceptos: pendiente, ordenada, gráfica, punto de corte con los ejes, intersección de dos funciones, rectas paralelas y perpendiculares. Finalmente, resolvemos problemas de aplicación. Matemáticas. Secundaria.

y resolver el sistema de ecuaciones.

Enlaces con problemas de funciones: