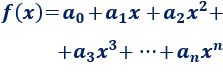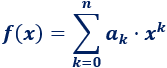La forma general de una función polinómica de grado n es
siendo an≠0.
Los términos ak se denominan coeficientes y an es el coeficiente principal.
También, podemos escribir la forma general como
El dominio de una función polinómica es el conjunto de todos los reales.
1. Función constante
Una función polinómica de grado 0 se denomina función constante y su forma general es
La gráfica de una función constante es una recta horizontal (paralela al eje de abscisas).
Corta el eje de ordenadas en un punto: (0, k). Sólo corta al eje de abscisas si k=0, en cuyo caso coincide con el eje.
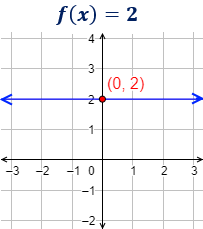
Ejemplo
El punto de corte con el eje de ordenadas es (0, 2). No corta al eje de abscisas.
2. Función lineal
Una función polinómica de grado 1 se denomina función lineal y tiene la forma general
El coeficiente m se denomina pendiente y el coeficiente n, ordenada en el origen.
La gráfica de una función lineal es una recta oblicua (recta no horizontal ni vertical).
Corta al eje de ordenadas en el punto (0, n). También, corta al eje de abscisas en un punto.
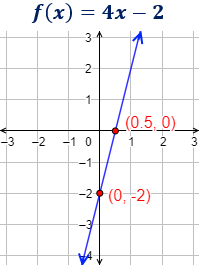
Ejemplo
La recta es creciente (de izquierda a derecha) porque la pendiente m=4 es positiva.
El punto de corte con el eje de abscisas es (0.5, 0) y con el eje de ordenadas es (0, -2).
Más información y ejemplos en función lineal.
3. Función cuadrática
Una función polinómica de grado 2 se denomina función cuadrática y tiene la forma general
La gráfica es una parábola. Tiene forma de si a>0 y forma de si a<0
Una función cuadrática corta al eje de ordenadas en el punto (0, c).
Puede cortar al eje de abscisas en dos, uno o ningún punto, dependiendo del número de soluciones reales de la ecuación cuadrática asociada, ax2 + bx + c = 0.
Toda función cuadrática presenta un extremo absoluto (máximo o mínimo) en
Este extremo se denomina vértice.
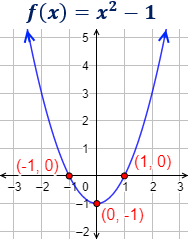
Ejemplo
El punto de corte con el eje de ordenadas es (0, -1). El vértice de la parábola también es (0, -1).
Los puntos de corte con el eje de abscisas son (-1,0) y (1,0). Observad que las primeras coordenadas son x=-1 y x=1, que son las soluciones de la ecuación cuadrática x2 – 1 = 0.
Más información y ejemplos en función cuadrática.
4. Función cúbica
Una función polinómica de grado 3 se denomina función cúbica y tiene la forma general
La gráfica es una curva cúbica.
Corta al eje de ordenadas en el punto (0, d).
Puede cortar al eje de abscisas en tres, dos o un punto, dependiendo de las soluciones de la ecuación cúbica asociada.
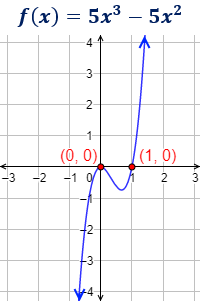
Ejemplo:
Los puntos de corte con el eje de abscisas son (0, 0) y (1, 0).
El punto de corte con el eje de ordenadas es (0, 0).
Enlaces con problemas:
- Dominio y recorrido (1)
- Dominio y recorrido (2)
- Funciones lineales
- Funciones cuadráticas
- Rectas y parábolas
- Funciones polinómicas
- Funciones definidas a trozos (1)
- Funciones definidas a trozos (2)
- Problemas de funciones (1)
- Problemas de funciones (2)
- Funciones continuas (1)
- Funciones continuas (2)
- Función inversa (1)
- Función inversa (2)
- Función inyectiva, sobreyectiva y biyectiva
- Asíntotas (1)
- Asíntotas (2)
- Máximos y mínimos (1)
- Máximos y mínimos (2)
- Criterio de la primera derivada
- Criterio de la segunda derivada
- Problemas de optimizar (1)
- Problemas de optimizar (2)
- Límites (1)
- Límites (2)
- Función par y función impar
- Cálculo de derivadas
- Teorema del emparedado