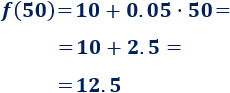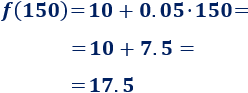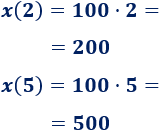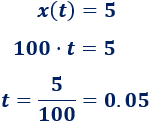Problemas de funciones

Vamos a resolver 3 problemas de funciones. Lo más importante es plantear la función, aplicarla para contestar a las preguntas e interpretar la gráfica.

Problema 1

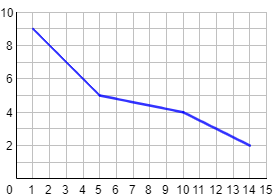
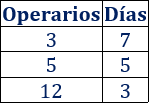
La siguiente función proporciona los días necesarios para construir un coche en función del número de operarios que trabajen:

Problemas resueltos de funciones: plantear funciones, representar e interpretar gráficas, calcular imágenes y antiimágenes. Problemas de aplicación. Matemáticas.

a. ¿Cuántos días se necesitan si trabajan 3 operarios? ¿Y si trabajan 5 operarios? ¿Y si trabajan 12 operarios?

b. ¿Cuántos operarios se necesitan para construir el coche en 4 días? ¿Y en 8 días?

c. ¿Se trata de una función lineal? ¿Por qué?

Solución:

a. Observando la gráfica,

Problemas resueltos de funciones: plantear funciones, representar e interpretar gráficas, calcular imágenes y antiimágenes. Problemas de aplicación. Matemáticas.

b. Para construirlo en 4 días, se necesitan 10 operarios. Para hacerlo en 8 días, se necesitan 2.

c. No. Las gráficas de las funciones lineales son rectas. La gráfica de este problema está formada por tres segmentos de rectas con distinta pendiente.

 

Problema 2

La compañía telefónica de Roberto le cobra 10€ mensuales de cuota y 0.05€ por cada minuto de llamada.

a. Calcular la función que proporciona el coste de la factura mensual de Roberto en función del número de minutos de llamada.

b. ¿Cuál sería el coste de un mes en el que ha realizado 50 minutos de llamada? ¿Y si son 150 minutos?

c. Si la factura del mes de junio fue de 20€, ¿cuánto minutos de llamada realizó Roberto?

Solución:

a. Si Roberto realiza llamadas con un total de x minutos, el coste de estas llamadas sería 0.05·x. Además de esto, hay que sumar 10€ de la cuota.

Por tanto, la función es

Problemas resueltos de funciones: plantear funciones, representar e interpretar gráficas, calcular imágenes y antiimágenes. Problemas de aplicación. Matemáticas.

b. Si en un mes realiza 50 minutos de llamadas, la factura de dicho mes será de 12.5€:

Problemas resueltos de funciones: plantear funciones, representar e interpretar gráficas, calcular imágenes y antiimágenes. Problemas de aplicación. Matemáticas.

Si son 150 minutos, será de 17.5€:

Problemas resueltos de funciones: plantear funciones, representar e interpretar gráficas, calcular imágenes y antiimágenes. Problemas de aplicación. Matemáticas.

c. Tenemos que calcular x tal que f(x) = 20:
Problemas resueltos de funciones: plantear funciones, representar e interpretar gráficas, calcular imágenes y antiimágenes. Problemas de aplicación. Matemáticas.

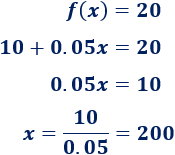
En el mes de junio realizó 200 minutos de llamada.

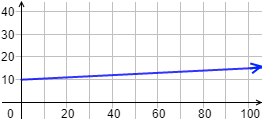
Gráfica de la función:

Problemas resueltos de funciones: plantear funciones, representar e interpretar gráficas, calcular imágenes y antiimágenes. Problemas de aplicación. Matemáticas.

Problema 3

La siguiente función proporciona la distancia (en kilómetros) que recorre una moto a una velocidad de 100km/h en función del tiempo t (en horas):

Problemas resueltos de funciones: plantear funciones, representar e interpretar gráficas, calcular imágenes y antiimágenes. Problemas de aplicación. Matemáticas.

a. ¿Qué distancia recorre en 2 horas? ¿Y en 5 horas?

b. ¿Cuánto tiempo debe circular para recorrer 5 kilómetros?

Solución:

 

a. Tenemos que calcular la imagen de 2 y de 5:

Problemas resueltos de funciones: plantear funciones, representar e interpretar gráficas, calcular imágenes y antiimágenes. Problemas de aplicación. Matemáticas.

En 2 horas recorre 200 kilómetros y en 5  horas, 500.

b. Tenemos que calcular t  tal que x(t)=5:

Problemas resueltos de funciones: plantear funciones, representar e interpretar gráficas, calcular imágenes y antiimágenes. Problemas de aplicación. Matemáticas.

Tarda 0.05 horas en recorrer 5km, es decir, 3 minutos.

 

Enlaces con problemas: