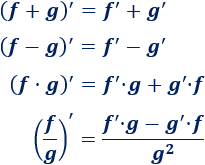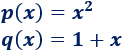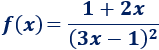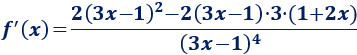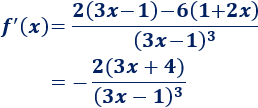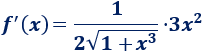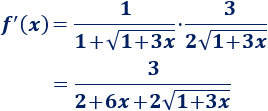Reglas de derivación
Dadas dos funciones f y g, las derivadas de su suma, resta, producto y cociente son
Si K es una constante y f es una función, la derivada de su producto es
Ejemplo:
Aplicamos la regla de la suma:
Regla de la cadena
La regla de la cadena proporciona la derivada de la composición de dos funciones f y g:
Ejemplo 1
Sea la función
Es composición de las siguientes funciones:
ya que
O, equivalentemente, f = p(q).
Las derivadas son
Por tanto, por la regla de la cadena,
Ejemplo 2
Tenemos que aplicar la regla del cociente y de la cadena (para el cuadrado):
Simplificamos:
Ejemplo 3
Si es necesario, se puede escribir la raíz como una potencia con exponente 1/2.
Aplicando la regla de la cadena,
Ejemplo 4
Aplicando la regla de la cadena,
Enlaces con problemas de funciones:
- Dominio y recorrido (1)
- Dominio y recorrido (2)
- Funciones lineales
- Funciones cuadráticas
- Rectas y parábolas
- Funciones polinómicas
- Funciones definidas a trozos (1)
- Funciones definidas a trozos (2)
- Problemas de funciones (1)
- Problemas de funciones (2)
- Funciones continuas (1)
- Funciones continuas (2)
- Función inversa (1)
- Función inversa (2)
- Función inyectiva, sobreyectiva y biyectiva
- Asíntotas (1)
- Asíntotas (2)
- Máximos y mínimos (1)
- Máximos y mínimos (2)
- Criterio de la primera derivada
- Criterio de la segunda derivada
- Problemas de optimizar (1)
- Problemas de optimizar (2)
- Límites (1)
- Límites (2)
- Función par y función impar
- Cálculo de derivadas
- Teorema del emparedado