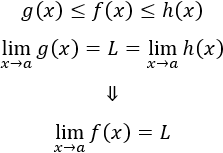El teorema del emparedado (también llamado teorema del sándwich, del bocadillo y de encaje, entre otros) es un resultado muy intuitivo y útil a la hora de calcular el límite de algunas funciones.
El teorema afirma que, si dos funciones tienen el mismo límite, entonces las funciones que están comprendidas entre éstas también tienen el mismo límite:
Ejemplo 1
Vamos a demostrar que
Como el seno toma valores en el intervalo [-1, 1],
Sólo tenemos que dividir entre x en esta relación para poder aplicar el teorema.
Como estamos calculando el límite cuando x tiende a +∞, podemos considerar x>0 y, por tanto, podemos dividir entre x sin cambiar los signos de desigualdad:
Como el límite de -1/x y el de 1/x coinciden y es igual a 0, por el teorema del emparedado, tenemos
Ejemplo 2
Vamos a demostrar que
Tenemos que multiplicar por x, pero como x tiende a 0, puede tomar valores positivos y negativos.
Si x>0, entonces
Por el teorema del emparedado,
De forma análoga, si x<0,
Por el teorema del emparedado,
Como los límites laterales coinciden,
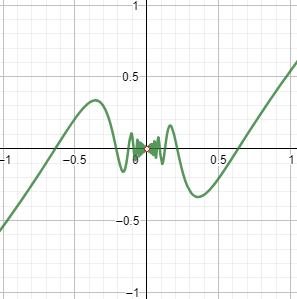
Gráfica de la función:
Enlaces con problemas de funciones:
- Dominio y recorrido (1)
- Dominio y recorrido (2)
- Funciones lineales
- Funciones cuadráticas
- Rectas y parábolas
- Funciones polinómicas
- Funciones definidas a trozos (1)
- Funciones definidas a trozos (2)
- Problemas de funciones (1)
- Problemas de funciones (2)
- Funciones continuas (1)
- Funciones continuas (2)
- Función inversa (1)
- Función inversa (2)
- Función inyectiva, sobreyectiva y biyectiva
- Asíntotas (1)
- Asíntotas (2)
- Máximos y mínimos (1)
- Máximos y mínimos (2)
- Criterio de la primera derivada
- Criterio de la segunda derivada
- Problemas de optimizar (1)
- Problemas de optimizar (2)
- Límites (1)
- Límites (2)
- Función par y función impar
- Cálculo de derivadas
- Teorema del emparedado