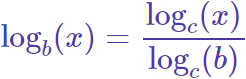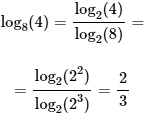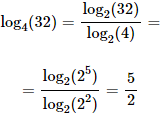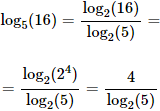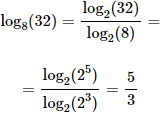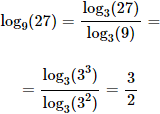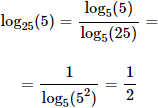En esta página proporcionamos la fórmula para cambiar la base de un logaritmo y algunos ejemplos de aplicación. Esta propiedad de los logaritmos nos permite operar entre logaritmos con bases distintas o calcular logaritmos.
1. Recordatorio
El logaritmo en base b de un número a se representa por logb(a) y es el número c que cumple bc = a:
- El número b es la base del logaritmo. Tiene que ser un real positivo distinto de 1.
- El número a es el argumento del logaritmo.
- El número c es el logaritmo en base b de a.
Si se sobreentiende, no es necesario escribir la base.
2. Cambio de base
La fórmula que nos permite cambiar de la base b a la base c es la siguiente:
Ejemplo:
Para poder calcular el logaritmo en base 8 de 4, podemos cambiar a base binaria (base 2):
Hemos escogido la base 2 porque tanto 4 como 8 son potencias de 2, lo que facilita el cálculo de los logaritmos.
3. Ejemplos
Ejemplo 1
Calcular el logaritmo en base 4 de 32:
Solución:
Pasamos a base 2 porque 32 y 4 son potencias de 2. Luego, escribimos 32 como 2 elevado a 5 y 4 como 2 elevado a 2:
Ejemplo 2
Pasar a logaritmo en base 2:
Solución:
Después de cambiar la base, escribimos 16 como 2 elevado a 4 para simplificar:
Ejemplo 3
Calcular el siguiente logaritmo:
Solución:
Como 8 y 32 son potencias de 2, pasamos a base 2:
Ejemplo 4
Calcular el siguiente logaritmo:
Solución:
Como 9 y 27 son potencias de 3, pasamos a base 3:
Ejemplo 5
Calcular el siguiente logaritmo:
Solución:
Pasamos a base 5:
Más ejemplos en cambio de base del logaritmo.
Otros temas de logaritmos: