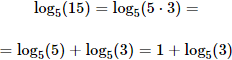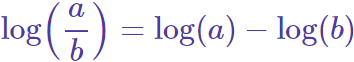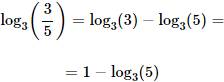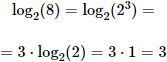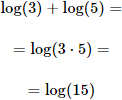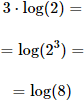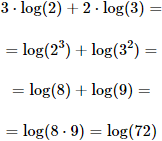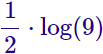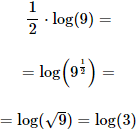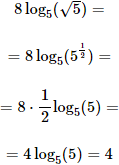En esta pagina enunciamos las propiedades de los logaritmos y las aplicamos para calcular operaciones entre logaritmos. No incluimos la propiedad de cambio de base.
1. Recordatorio
Es necesario que recordemos la definición de logaritmo:
El logaritmo en base b de un número a se representa por logb(a) y es el número c que cumple bc = a:
- El número b es la base del logaritmo. Tiene que ser un real positivo distinto de 1.
- El número a es el argumento del logaritmo.
- El número c es el logaritmo en base b de a.
Si se sobreentiende, no es necesario escribir la base.
2. Propiedades de los logaritmos
Logaritmo de un producto
El logaritmo de un producto de factores es la suma de los logaritmos de los factores:
Ejemplo:
Logaritmo de un cociente
El logaritmo de un cociente es el logaritmo del numerador menos el logaritmo del denominador:
Ejemplo:
Logaritmo de una potencia
El logaritmo de una potencia es el logaritmo de la base de la potencia multiplicado por el exponente:
Ejemplo:
Importante:
Observad que las bases de los logaritmos de las propiedades son iguales.
Ejemplo:
Podemos sumar logaritmos con base común:
No podemos sumar logaritmos con base distinta:
3. Ejemplos de aplicación
Ejemplo 1
Solución:
La suma de logaritmos es el logaritmo del producto:
Ejemplo 2
Solución:
El número 3 pasa al argumento como un exponente:
Ejemplo 3
Solución:
Antes de utilizar la propiedad de la suma de logaritmos, tenemos que introducir los coeficientes (3 y 2) como exponentes de los argumentos:
Ejemplo 4
Solución:
Recordad que el exponente 1/2 es la raíz cuadrada:
Por tanto, tenemos el logaritmo de una raíz cuadrada:
Ejemplo 5
Solución:
En lugar de introducir el 8 como un exponente, vamos a extraer el exponente 1/2 del argumento:
Más ejercicios similares en propiedades de los logaritmos.
Otros temas de logaritmos: