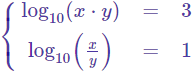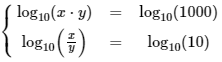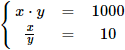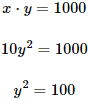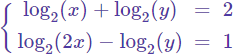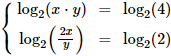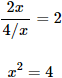En esta página resolvemos detalladamente dos sistemas de ecuaciones logarítmicas.
1. Introducción
Recordad que una ecuación logarítmica es una ecuación en la que la o las incógnitas aparecen multiplicando/dividiendo a logaritmos, en sus bases o en sus argumentos.
Un sistema de ecuaciones logarítmicas es un conjunto de ecuaciones logarítmicas cuya solución es solución de todas las ecuaciones logarítmicas.
Para poder resolver estos sistemas, necesitamos conocer las propiedades de los logaritmos (incluyendo el cambio de base) y las propiedades de las potencias.
2. Ejemplos de sistemas
Sistema 1
Solución:
El sistema está formado por dos ecuaciones con dos incógnitas (x e y).
Escribimos los términos independientes (3 y 1) como logaritmos en base 10 para tener igualdades entre logaritmos en la misma base: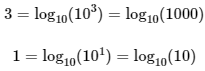
Reescribimos el sistema:
Dos logaritmos en la misma base son iguales si sus argumentos son iguales. Por tanto, podemos igualar los argumentos de los logaritmos de cada ecuación:
Observad que el sistema obtenido no es lineal, pero es fácil resolverlo, por ejemplo, por el método de sustitución.
De la segunda ecuación tenemos
Sustituimos en la primera:
Haciendo la raíz cuadrada, tenemos dos soluciones para y:
Sustituyendo en la primera ecuación, hallamos la otra incógnita: si y=10, entonces x=100; si y=-10, entonces x=-100.
Como los argumentos de los logaritmos del sistema inicial son positivos para las soluciones encontradas, el sistema tiene dos soluciones.
Una solución es
Y la otra es
Sistema 2
Solución:
Escribimos los términos independientes (2 y 1) como logaritmos en base 2:
Como tenemos todos los logaritmos en la misma base, podemos aplicar las propiedades de la suma y la resta de logaritmos:
Igualamos los argumentos y resolvemos el sistema (de ecuaciones no lineales) por el método de sustitución.
De la primera ecuación,
De la segunda,
Sustituimos y en la segunda:
Por tanto, tenemos las soluciones x=2 y x=-2. La negativa hay que descartarla porque haría que el argumento de un logaritmo sea negativo en el sistema inicial.
Por tanto, x=2 y, sustituyendo, y=2.
Así que la única solución del sistema de ecuaciones logarítmicas es
Más ejemplos en sistemas de ecuaciones logarítmicas.
Enlaces a problemas/ejercicios resueltos de logaritmos: